CHƯƠNG I: ĐA THỨC

Bài tập file word mức độ thông hiểu bài 13: Hình chữ nhật

2. THÔNG HIỂU (4 câu)

Câu 1. Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M,N lần lược là hình chiếu của O trên AB, BC. Chứng minh $MN=\frac{1}{2}AC$

Câu 2. Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F∈AB).

a) Chứng minh rằng tứ giác AEDF là hình chữ nhât.

b) Chứng minh rằng tứ giác BFED là hình bình hành.

Câu 3: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm dối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Câu 4: Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho $\widehat{AEB}=78^{\circ}$, $\widehat{EBC}=39^{\circ}$ Tính số đo của $\widehat{BEC}$ và $\widehat{EAB}$.

Câu 1.

Tứ giác MBNO có 3 góc vuông là OMB, MBN và ONB nên góc còn lại là NOM cũng là góc vuông. Vậy MBNO là hình chữ nhật.

=> MO = BN (1)

MO//BN (hay MO//CN) (2)

N là hình chiếu của O trên BC nên NB=NC (3)

Từ (1) và (3) => MO = NC. kết hợp với (2) suy ra OMNC là hình bình hành (tứ giác cócặp cạnh đối song song và bằng nhau)

=> MN = OC. Mà O là giao điểm 2 đường chéo của hình chữ nhật ABCD nên $OC=\frac{1}{2}AC$. Vậy $MN=\frac{1}{2}AC$ (đpcm)

Câu 2.

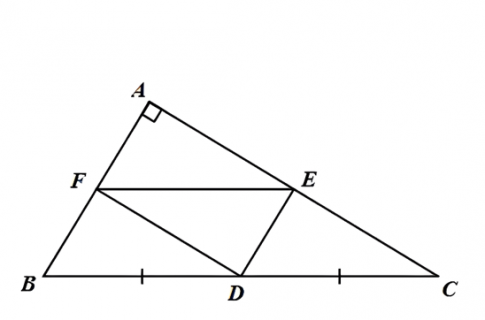
a) Tứ giác AEDF có:

AE // DF (AC // FD, E∈AC)

AF // DE (AB // DE, F∈AB)

⇒AEDF là hình bình hành.

Mà $\widehat{FAE}=90^{\circ}$ ΔABC vuông tại A)

Nên AEDF là hình chữ nhât.

b) ΔABC có D là trung điểm của BC và FD // AC ⇒F là trung điểm của AB.

ΔABC có D là trung điểm của BC và DE // AB ⇒E là trung điểm của AC

⇒ EFlà đường trung bình của tam giác ABC

⇒ EF//BC và $EF=\frac{1}{2}BC$

Lại có $BD=\frac{1}{2}BC$ (Vì D là trung điểm của BC)

⇒ EF//BD và EF=BD

Vậy tứ giác BFED là hình bình hành (dấu hiệu nhận biết).

Câu 3:

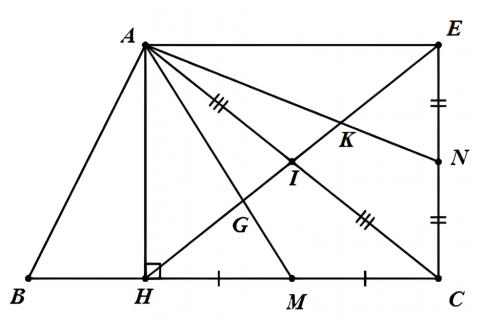
a) Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại I (gt)

I là trung điểm của AC (gt);

Và I là trung điểm của HE (E đối xứng với H qua I)

Do đó tứ giác AHCE là hình bình hành.

Mà $\widehat{AHC}=90^{\circ}$ (AH là đường cao của tam giác ABC)

Vậy tứ giác AHCE là hình chữ nhật.

b) MAHC có: HI là đường trung tuyến (I là trung điểm của AC)

Và AM là đường trung tuyến (M là trung điểm của HC)

Mà HI cắt AM tại G (gt)

Do đó G là trọng tâm của tam giác AHC ⇒ $HG=\frac{2}{3}HI$ và $GI=\frac{2}{3}HI$(1)

ΔAEC có hai đường trung tuyến AN và EI cắt nhau tại K.

⇒K là trọng tâm của tam giác AEC ⇒ $KE=\frac{2}{3}IE$ và $KI=\frac{2}{3}IE$ (2)

HI=IE (E đối xứng với H qua I) (3)

Từ (1), (2) và (3) suy ra $HG=KE=\frac{2}{3}IE$

Ta có: $GK=GI+IK=\frac{1}{3}IE+\frac{1}{3}IE=\frac{2}{3}IE$ suy ra $HG=KE=GK(=\frac{2}{3}IE)$

Câu 4:

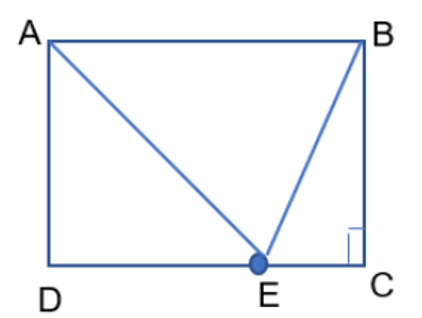
$Câu 4: Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho $\widehat{AEB}=78^{\circ}$, $\widehat{EBC}=39^{\circ}$ Tính số đo của $\widehat{BEC}$ và $\widehat{EAB}$.$