Bài tập file word mức độ nhận biết bài 13: Hình chữ nhật
1. NHẬN BIẾT (6 câu)
Câu 1: Chỉ được sử dụng compa, hãy kiểm tra tứ giác ở hình sau có phải là hình chữ nhật hay không.

Câu 2: Cho hình 15. Vẽ thêm điểm P để tứ giác MNPQ là hình chữ nhật.

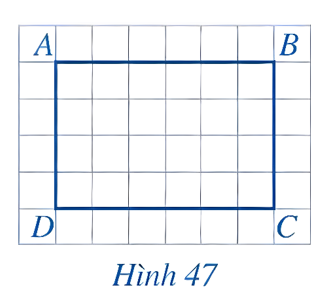
Câu 3: Cho biết số đo mỗi góc của tứ giác ABCD trong hình 47.
Câu 4:
a) Mỗi hình chữ nhật có là một hình thang cân hay không?
b) Mỗi hình chữ nhật có là một hình bình hành hay không?
Câu 5. Cho hình thang cân ABCD có AB // CD, Aˆ=90∘. Chứng minh ABCD là hình chữ nhật.
Câu 6. Cho tam giác ABC vuông tại A có M là trung điểm cúa cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh tứ giác ABDC là hình chữ nhật và $AM=\frac{1}{2}BC$
Câu 1:
- Ta kiểm tra các cặp cạnh đối xem chúng có bằng nhau không
Nếu các cặp cạnh đối bằng nhau ⇒ ABCD là hình bình hành
- Sau đó: Kiểm tra hai đường chéo xem chúng bằng nhau không
Nếu hai đường chéo bằng nhau ⇒ ABCD là hình chữ nhật
Câu 2:
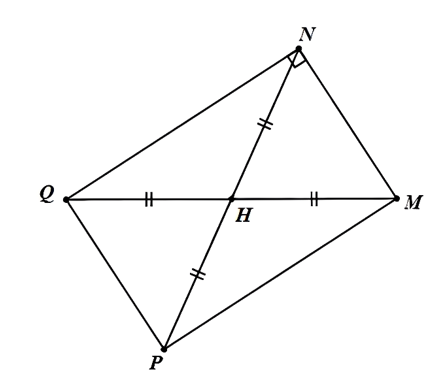
Trên tia đối của tia HM lấy điểm P sao cho HP=HM
Chứng minh:
Tứ giác MNQP có QN và MP cắt nhau tại trung điểm của mỗi đường.
Do đó tứ giác MNQP là hình bình hành (dấu hiệu nhận biết)
Mặt khác $\widehat{NMQ}=90^{\circ}$ (gt) ⇒ Tứ giác MNQP là hình chữ nhật (dấu hiệu nhận biết).
Câu 3:
Số đo mỗi góc của tứ giác ABCD trong hình 47 đều bằng 90o
Câu 4:
a) Mỗi hình chữ nhật có là một hình thang cân.
b) Mỗi hình chữ nhật có là một hình bình hành.
Câu 5.
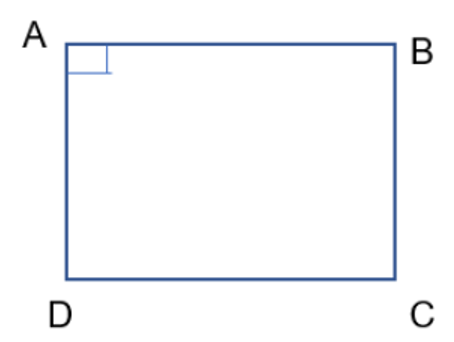
ABCD là hình thang cân và AB//CD nên:
2 góc kề đáy AB là: $\widehat{A}=\widehat{B}=90^{\circ}$
$\Rightarrow \widehat{C}+\widehat{D}=360^{\circ}-(\widehat{A}+\widehat{B})=360^{\circ}-(90^{\circ}+90^{\circ})=180^{\circ}$
2 góc kề đáy CD là $\widehat{C}=\widehat{D}\Rightarrow \widehat{C}=\widehat{D}=12.180^{\circ}=90^{\circ}$
=> Tứ giác ABCD có 4 góc vuông nên là hình chữ nhật.
Câu 6.
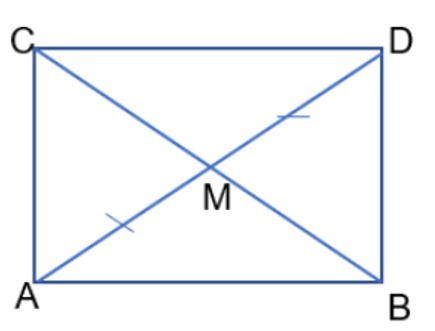
Trên tia đối của tia MA lấy điểm D sao cho MD = MA M là trung điểm của AD. Tứ giác ABCD có 2 đường chéo là AD và BC cắt nhau tại trung điểm của mỗi đường nên là hình bình hành. Lại có góc A vuông nên là hình chữ nhật (đpcm)
2 đường chéo AD = BC. Mà $AM=\frac{1}{2}AD$ nên $AM=\frac{1}{2}BC$ (đpcm )

Bình luận