Câu hỏi tự luận mức độ vận dụng Toán 9 ctst bài 2: Phương trình bậc hai một ẩn

Câu 1: 

a) Tìm để phương trình có nghiệm

Xét 2 tường hợp

TH1: Với phương trình trở thành:

Vậy thỏa yêu cầu bài toán

TH2: Với phương trình là một phương trình bậc hai và có

để phương trình có nghiệm thì

Kết hợp hai trường hợp suy ra phương trình (1) có nghiệm khi và chỉ khi

b) Tìm để phương trình có hai nghiệm phân biệt

để phương trình có hai nghiệm phân biệt thì và

hay và

hay và

Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi và

Câu 2: 

Ta có:

a) Phương tình có hai nghiệm phân biệt khi và hay    và

b) Xét Phương trình có nghiệm kép khi và hay 

c) Ta tìm được

d) Ta tìm được

e) Ta tìm được

Câu 3: 

Ta có

 mà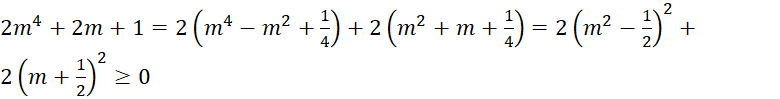

Dấu “=” xảy ra khi và suy ra vô lý

Vậy phương trình luôn có hai nghiệm phân biệt.

Câu 4: 

a. Học sinh tự làm nhé

b. Xét phương trình hoành độ giao điểm của (d)  và (P):

=

Phương trình (1) có với mọi m. Phương trình (1) luôn có hai nghiệm phân biệt. Do đó (d) luôn cắt (P) tại hai điểm phân biệt.

Câu 5: 

giao điểm với tại 2 điểm nằm về hai phía của trục tung

Tọa độ giao điểm là nghiệm của phương trình:

cắt tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu.

.

Vậy thì cắt d tại hai điểm nằm về hai phía của trục tung.

Câu 7:

a Tìm m để đường thẳng đi qua

Do (d) đi qua Thay vào phương trình đường thẳng  ta được: 

Vậy với m = 2 thì đường thẳng đi qua

b  Tìm m để đường thẳng tiếp xúc với Parabol

Phương trình hoành độ giao điểm của (d) và (P) là

Để tiếp xúc với Parabol thì phương trình (*) có nghiệm kép hay

hoặc

Vậy hoặc

Câu 8: 

Gọi chiều rộng mảnh vườn là , điều kiện: .

Khi đó, chiều dài mảnh vườn là

Diện tích mảnh vườn là:

Theo đề bài, ta có phương trình: 

Giải phương trình, ta được: (nhận);  (loại)

Vậy chiều rộng mảnh vườn là , chiều dài mảnh vườn là .

Câu 9: 

Đổi phút giờ

Gọi vận tốc ô tô dự định đi trên quãng đường là

Thời gian dự định đi trên quãng đường là

Vận tốc thực tế ô tô đi là

Nên thời gian thực tế đi hết quãng đường là

Vì xe đến B chậm hơn dự định phút nên ta có phương trình :

Ta có nên phương trình có hai nghiệm phân biệt 

Vậy vận tốc dự định là 50km/h và thời gian dự định là giờ

Câu 10: 

Gọi thời gian đội thứ nhất hoàn thành công việc là (ngày)

Suy ra thời gian đội thứ hai hoàn thành công việc là (ngày)

Trong 1 ngày đội I làm được (công việc), đội II làm được( công việc).

Vì hai người hoàn thành công việc trong 12 ngày nên ta có phương trình:

phương trình có hai nghiệm phân biệt (thỏa mãn); (loại)

Vậy thời gian đội thứ nhất hoàn thành công việc là 20 (ngày)

Thời gian đội thứ hai hoàn thành công việc là 30 (ngày).