I. XÁC SUẤT CỦA BIẾN CỐ TRONG TRÒ CHƠI TUNG ĐỒNG XU

HĐ1

a) Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là A = {S; N}. 

b) B = {N}

Có 1 kết quả thuận lợi cho biến cố B là: mặt N.

c) Tỉ số của số các kết quả thuận lợi cho biến cố B trên và số phần tử của tập hợp A là: $\frac{1}{2}$

Ghi nhớ: Trong trò chơi tung đồng xu, ta có:

• Xác suất của biến cố ”Mặt xuất hiện của đồng xu là mặt N” bằng $\frac{1}{2}$.
• Xác suất của biến cố ”Mặt xuất hiện của đồng xu là mặt S” bằng $\frac{1}{2}$.

Chú ý: Trong trò chơi tung đồng xu  trên, số các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là 2. Xác suất của mỗi biến cố đó bằng $\frac{1}{2}$.

II. XÁC SUẤT CỦA BIẾN CỐ TRONG TRÒ CHƠI VÒNG QUAY SỐ

HĐ2:

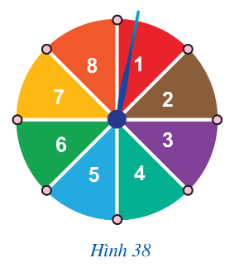
a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện ghi trên hình quạt là C = {1; 2; 3;4;5;6;7;8}. 

b) D = {1; 3; 5; 7}.

Có bốn kết quả thuận lợi cho biến cố là: 1, 3, 5, 7. 

c) Tỉ số cần của số các kết quả thuận lợi cho biến cố D và số phần tử của tập hợp C là: $\frac{4}{8}=\frac{1}{2}$

Lưu ý: Trong trò chơi quay số đã nêu, tỉ số giữa số các kết quả thuận lợi cho biến cố “Chiếc kim chỉ vào hình quạt ghi số lẻ” và số các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào là $\frac{4}{8}=\frac{1}{2}$. Tỉ số này gọi là xác suất của biến cố nói trên.

Ghi nhớ: Trong trò chơi vòng quay số đã nêu, nếu k là số kết quả thuận lợi cho một biến cố thì xác suất của biến cố đó bằng $\frac{k}{8}$.

Ví dụ 1: (SGK – tr.27)

Hướng dẫn giải (SGK – tr.27)

Luyện tập 1

Tập hợp gồm các kết quả có thể xảy ra  là:  {1; 2; 3; 4; 5; 6; 7; 8}

Có 5 kết quả thuận lợi cho biến cố “Chiếc kim chỉ vào hình quạt ghi số nhỏ hơn 6” là: 1, 2, 3, 4, 5.

Vì thế, xác suất của biến cố trên là: $\frac{5}{8}$.

III. XÁC SUẤT CỦA BIẾN CỐ TRONG TRÒ CHƠI CHỌN NGẪU NHIÊN MỘT ĐỐI TƯỢNG TỪ MỘT NHÓM ĐỐI TƯỢNG

HĐ3

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện ghi trên viên bi là:

E = {Lúa, Ngô, Hoa Hồng, Hoa Hướng Dương, Trâu, Bò, Voi, Hổ, Báo, Sư tử}.

b) G có sáu kết quả thuận lợi cho biến cố là: Trâu, Bò, Voi, Hổ, Báo, Sư tử.

c) Tỉ số cần của số các kết quả thuận lợi  cho biến cố G và số phần tử của tập hợp E là: $\frac{6}{10}=\frac{3}{5}$

Lưu ý: Trong trò chơi lấy bi từ trong hộp đã nêu, tỉ số giữa số các kết quả thuận lợi cho biến cố "Trên viên bi lấy ra viết tên một loài động vật" và số các kết quả có thể xảy ra đối với tên sinh vật được viết trên viên bi là $\frac{6}{10}$ = 0,6. Tỉ số này gọi là xác suất của biến cố nói trên.

Ghi nhớ: Trong trò chơi chọn ngẫu nhiên một đối tượng từ một nhóm đối tượng, xác suất của biến cố bằng tỉ số của số kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với đối tượng được chọn ra.

Ví dụ 2: (SGK – tr.27)

Hướng dẫn giải (SGK – tr.27)

Ví dụ 3: (SGK – tr.28)

Hướng dẫn giải (SGK – tr.28)

Ví dụ 4: (SGK – tr.28)

Hướng dẫn giải (SGK – tr.28)

Luyện tập 2

Tập hợp gồm các kết quả có thể xảy ra là: M = {10; 11; 12; 13;…; 99}. Tập hợp A có 90 phần tử.

Có 10 kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là một số chia hết cho 9 dư 1” là: 10, 19, 28, 38, 46, 55, 64, 73, 82, 91.

Vì thế, xác suất của biến cố trên là: $\frac{10}{90}=\frac{1}{9}$