I. SỐ TRUNG BÌNH CỘNG (SỐ TRUNG BÌNH)

1. Định nghĩa

HĐ1: 

Trung bình cộng của 5 số trên là: 

$\overline{X}= \frac{165+172+172+171+170}{5}= 170$

Kết luận:

Số trung bình cộng của một mẫu $n$ số liệu thống kê bằng tổng của các số liệu chia cho số các số liệu đó. Số trung bình cộng $\overline{x}$ của mẫu số liệu $x_1, x_2,…,x_n$ là: 

$\overline{x}= \frac{x_1+ x_2+ …+ x_n}{n}$

Ví dụ 1 (SGK – tr27)

Nhận xét:

Ta có thể tính số trung bình cộng theo các công thức sau:

+ Số trung bình cộng $\overline{x}$ của mẫu số liệu thống kê trong bảng phân bố tần số là: 

$\overline{x}= \frac{n_1x_1+ n_2x_2+ …+ n_kx_k}{n_1+ n_2+…+n_k}$

+ Số trung bình cộng $\overline{x}$ của mẫu số liệu thống kê trong bảng phân bố tần số tương đối là:

$\overline{x}= f_1x_1+ f_2x_2+…+f_kx_k$

Trong đó $f_1 = \frac{n_1}{n}, f_2 = \frac{n_2}{n},…, f_k = \frac{n_k}{n}$, với $n = n_1 + n_2 + … + n_k.$

Luyện tập 1:

Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.

Số bàn thắng trung bình trong mỗi trận đấu $= \frac{6+6+2+1+2+4+3}{7}= 3,43$

2. Ý nghĩa:

Khi các số liệu trong mẫu ít sai lệch với số trung bình cộng, ta có thể giải quyết được vấn đề trên bằng cách lấy số trung bình cộng làm đại diện cho mẫu số liệu này. 

II. TRUNG VỊ

Định nghĩa

HĐ2:

Số trung bình cộng của mẫu số liệu trên là:

$\overline{x}= \frac{1+1+3+6+7+8+8+9+10}{9} ≈ 5,9$

Quan sát mẫu số liệu ta thấy nhiều số liệu có sự chênh lệch lớn so với số trung bình cộng. Vì vậy, ta không thể lấy số trung bình cộng làm đại diện cho mẫu số liệu mà ta phải chọn số đặc trưng khác thích hợp hơn. Cụ thể, ta chọn số đứng chính giữa mẫu số liệu, tức là số 7 làm đại diện cho mẫu số liệu đó. 

Kết luận:

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm (hoặc không tăng). 

+ Nếu $n$ là số lẻ thì số liệu đứng ở vị trí thứ $\frac{n+1}{2}$ (số đứng chính giữa) gọi là trung vị.

+ Nếu $n$ là số chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ $\frac{n}{2}$ và $\frac{n}{2} + 1$ gọi là trung vị.

Trung vị kí hiệu là $M_e.$

Ví dụ 2 (SGK – tr29)

Luyện tập 2: 

+ Sắp xếp mẫu số liệu theo thứ tự không giảm: $23, 23, 25, 26$

+ Mẫu số liệu có 4 số liệu nên trung vị của mẫu số liệu là: $M_e = \frac{23+25}{2}= 24$

Nhận xét:

+ Trung vị không nhất thiết là một số trong mẫu số liệu và dễ tính toán.

+ Khi các số liệu trong mẫu không có sự chênh lệch lớn thì số trung bình cộng và trung vị xấp xỉ nhau. 

2. Ý nghĩa:

Nếu những số liệu trong mẫu có sự chênh lệch lớn thì ta nên chọn thêm trung vị làm đại diện cho mẫu số liệu đó nhằm điều chỉnh một số hạn chế khi sử dụng số trung bình cộng.

III. TỨ PHÂN VỊ

1. Định nghĩa

HĐ3:

Trung vị của mẫu số liệu trên là $M_e = 6.$ 

Kết luận:

Sắp thứ tự mẫu số liệu gồm $n$ số liệu thành một dãy không giảm.

Tứ phân vị của mẫu số liệu trên là bộ ba giá trị: tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phần tử bằng nhau. 

+ Tứ phân vị thứ hai $Q_2$ bằng trung vị.

+ Nếu n là số chẵn thì tứ phân vị thứ nhất $Q_1$ bằng trung vị của nửa dãy phía dưới và tứ phân vị thứ ba $Q_3$ bằng trung vị của nửa dãy phía trên. 

+ Nếu $n$ là số lẻ thì tứ phân vị thứ nhất $Q_1$ bằng trung vị của nửa dãy phía dưới (không bao gồm $Q_2$) và tứ phân vị thứ ba $Q_3$ bằng trung vị của nửa dãy phía trên (không bao gồm $Q_2$). 

Ví dụ 3 (SGK – tr31)

Luyện tập 3:

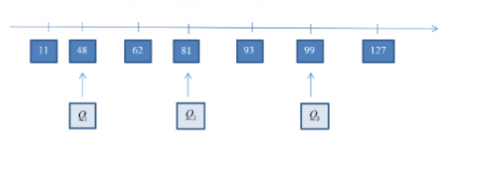
+ Sắp xếp mẫu số liệu trên theo thứ tự không giảm: $11, 48, 62, 81, 93, 99, 127$

+ Trung vị của mẫu số liệu là: $Q_2 = 81$

+ Trung vị của dãy $11, 48, 62$ là: $Q_1 = 48$

+ Trung vị của dãy $93, 99, 127$ là: $Q_3 = 99$

Biểu diễn tứ phân vị trên trục số:

2. Ý nghĩa:

Trong thực tiễn, bằng cách lấy thêm trung vị của từng dãy số liệu tách ra bởi trung vị của mẫu số liệu mà nhiều số liệu trong mẫu có sự chênh lệch lớn so với trung vị, ta nhận được tứ phân vị đại diện cho mẫu số liệu đó.

IV. MỐT

1. Định nghĩa

HĐ4:

Cỡ áo mà cửa hàng bác Tâm bán được nhiều nhất trong tháng đầu tiên là cỡ áo: 40. 

Kết luận:

Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là $M_o.$ 

Chú ý: 

Một mẫu số liệu có thể có một hoặc nhiều mốt.

Ví dụ 4 (SGK – tr32)

Luyện tập 4:

a. Ta lập bảng tần số:

Từ bảng tần số ta thấy mốt của mẫu số liệu trên là: $M_o = 5.$

b. Tỉ lệ số học sinh lớp $10A$ đạt điểm từ 8 trở lên là: $\frac{5+5+2}{40} = 0,3 = 30%$

Tỉ lệ này cho thấy số học sinh đạt điểm giỏi của lớp $10A$ là $30%.$ 

Ý nghĩa:

Mốt của một mẫu số liệu đặc trưng cho số lần lặp đi lặp lại nhiều nhất tại một vị trí của mẫu số liệu đó. Dựa vào mốt, ta có thể đưa ra những kết luận (có ích) về đối tượng thống kê.  

V. TÍNH HỢP LÍ CỦA SỐ LIỆU THỐNG KÊ

HĐ5:

Sau khi thu thập, tổ chức, phân loại và biểu diễn số liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các số liệu đó để xem xét tính hợp lí của số liệu thống kê, đặc biệt chỉ ra được những số liệu bất thường (hay còn gọi là dị biệt, trong tiếng Anh là Outliers). Ta có thể sử dụng các số liệu đặc trưng đo xu thế trung tâm.  

Ví dụ 5 (SGK – tr33)

Chú ý:

Trong thực tiễn, những số liệu bất thường của mẫu số liệu được xác định bằng những công cụ toán học sâu sắc hơn.