I. SỐ GẦN ĐÚNG

HĐ1:

Bác Mai không thể thanh toán bằng tiền mặt cho người thu tiền điện số tiền chính xác là 763 951 đồng bởi vì chỉ có mệnh giá tiền lẻ đến mức “nghìn đồng”

Kết luận: 

Trong đo đạc và tính toán, ta thường chỉ nhận được số gần đúng.

II. SAI SỐ CỦA SỐ GẦN ĐÚNG

1. Sai số tuyệt đối

HĐ2:

1. Công thức tính diện tích S của bồn hoa là: $S= \pi.R^2= \pi.0,8^2 (m^2)$
2. Giá trị $\left | S-1,984 \right |$ biểu diễn độ lệch giữa số $1,984$ và $S.$  

Kết luận:

Nếu $a$ là số gần đúng của số đúng $\overline{a}$ thì $∆_a= \left | \overline{a} - a \right |$ được gọi là sai số tuyệt đối của số gần đúng a (Hình 1). 

Ví dụ 1 (SGK – tr22)

Chú ý: 

Sai số tuyệt đối của số gần đúng nhận được trong một phép đo đạc, tính toán càng bé thì kết quả của phép đo đạc, tính toán đó càng chính xác. 

2. Độ chính xác của một số gần đúng

HĐ3: 

Để ước lượng sai số tuyệt đối đó, ta làm như sau: Do $3,1 < \pi < 3,15$ nên $3,1.(0,8)^2 < \pi.(0,8)^2 < 3,15.(0,8)^2$

Suy ra $1,984 < S < 2,016.$

Vậy $∆_{S1}= \left | S - S_1 \right | < 2,016 – 1,984 = 0,032.$

Ta nói: Kết quả của bạn Ngân có sai số tuyệt đối không vượt quá $0,032$ hay có độ chính xác là $0,032.$ 

Nhận xét:

Giả sử $a$ là số gần đúng của số đúng $\overline{a}$ sao cho 

$∆_a= \left | \overline{a}-a \right | ≤ d ⟺ -d ≤ \overline{a}-a ≤ d ⟺ a-d ≤ \overline{a} ≤ a+d$

Kết luận:

Ta nói $a$ là số gần đúng của $\overline{a}$ với độ chính xác $d$ nếu $∆_a= \left | \overline{a}-a \right |≤d$ và quy ước viết gọn là $\overline{a}= a ± d$

Nhận xét: 

Nếu $∆_a ≤ d$ thì số đúng $\overline{a}$ nằm trong đoạn $[a – d; a + d]$. Bởi vậy, $d$ càng nhỏ thì độ sai lệch của số gần đúng $a$ so với số đúng $\overline{a}$ càng ít. Điều đó giải thích vì sao $d$ được gọi là độ chính xác của số gần đúng. 

Ví dụ 2 (SGK – tr23)

3. Sai số tương đối

HĐ4:

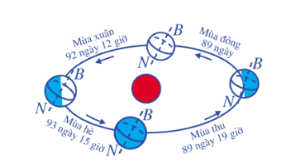
Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá $\frac{1}{4}$ ngày, có nghĩa là không vượt quá $360$ phút. 

Phép đo của Hùng có sai số tuyệt đối không vượt quá 1 phút. 

Nếu chỉ so sánh $360$ phút và $1$ phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, $\frac{1}{4}$ ngày hay $360$ phút là độ chính xác của phép đo một chuyển động trong $365$ ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong $15$ phút. So sánh hai tỉ số $\frac{\frac{1}{4}}{365}= \frac{1}{1 460}= 0,0006849…$ và $\frac{1}{15}= 0,0666…$, ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều. 

Kết luận:

Ngoài sai số tuyệt đối $∆_a$ của số gần đúng $a$, người ta còn xét một tỉ số khác liên quan đến sai số. 

Tỉ số $\Delta= \frac{∆_a}{\left | a \right | }$ được gọi là sai số tương đối của số gần đúng $a$. 

Nhận xét: 

+ Nếu $\overline{a}= a ± d$ thì $∆_a ≤ d$. Do đó $\Delta \leq \frac{d}{\left | a \right | }$. Vì vậy, nếu $\frac{d}{\left | a \right | }$ càng bé thì chất lượng của phép đo đạc, tính toán càng cao. 

+ Người ta thường viết sai số tương đối dưới dạng phần trăm. Chẳng hạn, trong phép đo thời gian Trái Đất quay một vòng xung quanh Mặt Trời thì sai số tương đối không vượt quá 

$\frac{\frac{1}{4}}{365}= \frac{1}{1 460}= 0,068%$

III. SỐ QUY TRÒN. QUY TRÒN SỐ ĐÚNG VÀ SỐ GẦN ĐÚNG

1. Số quy tròn. 

Kết luận:

Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu. 

2. Quy tròn số đến một hàng cho trước. 

HĐ5:

Khi quy tròn số $3,141$ đến hàng phần trăm ta được số $3,14$ và sai số tuyệt đối của số quy tròn là $\left | 3,141 - 3,14 \right |= 0,001<0,005$. Do vậy, số quy tròn $3,14$ là số gần đúng của $3,141$ với độ chính xác $0,005$. 

Nhận xét: 

Khi quy tròn số nguyên hoặc số thập phân đến một hàng cho trước thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Như vậy, ta có thể lấy độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn. 

Quy tròn số gần đúng căn cứ vào độ chính xác cho trước.

HĐ6:

Yêu cầu ở câu a là quy tròn đến hàng phần trăm còn yêu cầu ở câu b chỉ yêu cầu quy tròn tức là ta phải quy tròn số với độ chính xác đã cho. 

Quy ước:

Cho $a$ là số gần đúng với độ chính xác $d$. Giả sử $a$ là số nguyên hoặc số thập phân. Khi được yêu cầu quy tròn số $a$ mà không nói rõ quy tròn đến hàng nào thì ta quy tròn số $a$ đến hàng thấp nhất mà $d$ nhỏ hơn một đơn vị của hàng đó. 

Ví dụ 3 (SGK – tr25)

Luyện tập 1:

+ Ta có: $0,0000 < d = 0,0001 < 0,001$ nên hàng thấp nhất mà $d$ nhỏ hơn một đơn vị của hàng đó là hàng phần nghìn.

+ Vậy ta quy tròn a đến hàng phần nghìn. Số quy tròn của $a$ là: $28,416$. 

HĐ7:

Để thực hiện phép tính $3^7.\sqrt{14}$ ra kết quả có bốn chữ số ở phần thậo phân, ta có thể làm như sau:

+ Ấn liên tiếp 

+ Tiếp tục ấn lần lượt  thì màn hình hiện ra Fix 0 ~ 9?

Ấn tiếp  để lấy bốn chữ số thập phân. Kết quả hiện ra màn hình là $8183.0047$. 

Luyện tập 2:

Sử dụng máy tính cầm tay, ta tính được kết quả là: $\sqrt[3]{15}: 5 - 2 ≈-1,51$

Luyện tập 3:

+ Khối lượng của Trái Đất là: $5,9722. 10^{24}$ (kg).

+ Khối lượng của Mặt Trời là: $1,9891. 10^{30}$ (kg).

Ví dụ 4 (SGK – tr26).