Đề thi cuối kì 2 toán 10 CD: Đề tham khảo số 6

Trọn bộ Đề thi cuối kì 2 toán 10 CD: Đề tham khảo số 6 bộ sách mới Cánh diều gồm nhiều câu hỏi ôn tập hay, các dạng bài tập phong phú giúp các em củng cố ôn luyện lại kiến thức thật tốt chuẩn bị tốt cho kì thi sắp tới. Tài liệu có kèm theo đáp án và lời giải chi tiết. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt điểm cao. Thầy cô và các em kéo xuống để tham khảo ôn luyện

PHÒNG GD & ĐT ……………….	Chữ kí GT1: ...........................
TRƯỜNG THCS……………….	Chữ kí GT2: ...........................

ĐỀ KIỂM TRA CUỐI HỌC KÌ 2

TOÁN 10 - CÁNH DIỀU

NĂM HỌC: 2022 - 2023

Thời gian làm bài: 90 phút (Không kể thời gian phát đề)

Họ và tên: …………………………………… Lớp: ………………..

Số báo danh: …………………………….……Phòng KT:…………..

Mã phách

Điểm bằng số

Điểm bằng chữ

Chữ ký của GK1

Chữ ký của GK2

Mã phách

A. PHẦN TRẮC NGHIỆM (7 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:

Câu 1: Cho hai vectơ và khác là góc tạo bởi 2 vectơ và khi . Chọn khẳng định đúng.
A. .
B. .
C. .
D. .

Câu 2: Đo chiều dài của một cây thước, ta được kết quả . Khi đó sai số tuyệt đối của phép đo được ước lượng là
A. .
B. .
C. .
D. .

Câu 3: Điểm thi tuyển sinh vào lớp 10 ba môn Toán, Văn, Tiếng Anh của một học sinh lần lượt là 8,. Điểm thi trung bình ba môn thi của học sinh đó là
A. 8,0 .
B. 23,7 .
C. 7,7 .
D. 7,9 .

Câu 4: Mẫu số liệu sau cho biết cân nặng (đơn vị kg) của các học sinh Tổ 1 lớp

Khoảng biến thiên của mẫu số liệu này là
A. 38 .
B. 20 .
C. 42 .
D. 22 .

Câu 5: Cho mẫu số liệu . Độ lệch chuẩn của mẫu gần bằng
A. 8 .
B. 2,8 .
C. 2,4 .
D. 6 .

Câu 6: Trong mặt phẳng , cho tam giác biết . Gọi là điểm thuộc cạnh sao cho . Tính độ dài của vec tơ .
A. .
B. .
C. .
D. .

Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là . Sai số tương đối tối đa trong phép đo là bao nhiêu?
A. .
B. .
C. .
D. .

Câu 8: Tìm tứ phân vị của mẫu số liệu sau

A. .
B. .
C. .
D. .

Câu 9: Phương trình tổng quát của đường thẳng đi qua điểm và có vectơ pháp tuyến là
A. .
B. .
C. .
D. .

Câu 10: Trong mặt phẳng tọa độ , phương trình tổng quát của đường thẳng đi qua hai điểm và là
A. .
B. .
C. .
D. .

Câu 11: Tính góc giữa hai đường thẳng và
A. .
B. .
C. .
D. .

Câu 12: Khoảng cách từ điểm đến đường thẳng nằm trong khoảng nào sau đây?
A. .
B. .
C. .
D. .

Câu 13: Trong mặt phẳng với hệ trục cho đường tròn . Đường tròn có toạ độ tâm và bán kính bằng
A. .
B. .
C. .
D. .

Câu 14: Trong mặt phẳng với hệ toạ độ , phương trình đường tròn có tâm và đi qua điểm là
A. .
B. .
C. .
D. .

Câu 15: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A. .
B. .
C. .
D. .

Câu 16: Trường THPT , khối 12 có 11 lớp, khối 11 có 10 lớp và khối 10 có 12 lớp. Thầy Tổ trưởng tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn?
A. 3 .
B. 33 .
C. 11 .
D. 10 .

Câu 17: Trong tủ quần áo của bạn Ngọc có 10 cái áo sơ mi đôi một khác nhau và 5 cái chân váy với hoa văn khác nhau. Bạn Ngọc muốn chọn ra một bộ quần áo để đi dự tiệc sinh nhật. Hỏi bạn Ngọc có bao nhiêu cách chọn?
A. 10 .
B. 50 .
C. 5 .
D. 15 .

Câu 18: Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế?
A. 4 cách.
B. 8 cách.
C. 12 cách.
D. 24 cách.

Câu 19: Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư?
A. .
B. 35 !.
C. .
D. .

Câu 20: Cho tập hợp . Số tập con gồm 2 phần tử của là
A. 10 .
B. 8 .
C. 16 .
D. 20 .

Câu 21: Trong khai triển nhị thức Niu-tơn của có bao nhiêu số hạng?
A. 6 .
B. 3 .
C. 5 .
D. 4 .

Câu 22: Có 2020 tấm thẻ được đánh số từ 1 đến 2020. Xét phép thử: lấy ngẫu nhiên 5 tấm thẻ trong số 2020 tấm thẻ đã cho. Tính số phấn tử của không gian mẫu.
A. .
B. .
C. .
D. .

Câu 23: Một tổ học sinh gồm có 5 học sinh nữ và 7 học sinh nam, chọn ngẫu nhiên 2 học sinh. Tính xác suất để 2 học sinh được chọn có cả học sinh nam và học sinh nữ?
A. .
B. .
C.
D.

Câu 24: Từ một hộp chứa 10 quả cầu màu đỏ và 5 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng
A. .
B. .
C. .
D. .

Câu 25: Trong mặt phẳng , phương trình tổng quát của đường thẳng đi qua điểm và song song đường thẳng có phương trình: là
A. .
B. .
C. .
D. A.

Câu 26: Với giá trị nào của thì hai đường thẳng

A. .
B. .
C. .
D. .

Câu 27: Trong mặt phẳng , đường tròn đi qua ba điểm có phương trình là.
A. .
B. .
C. .
D. .

Câu 28: Cho đường tròn và điểm . Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn tại điểm .
A. .
B. .
C. .
D. .

B. PHẦN TỰ LUẬN (3 điểm)

Câu 1: (1 điểm)

Mật khẩu mở điện thoại của bác Bình là một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn 600.000. Bạn An được bác Bình cho biết thông tin ấy nhưng không cho biết mật khẩu chính xác là số nào nên quyết định thử bấm ngẫu nhiên một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn 600.000. Tính xác suất để bạn An nhập một lần duy nhất mà đúng mật khẩu để mở được điện thoại của bác Bình.

Câu 2 (0,5 điểm): Cho đa giác đều có 48 đỉnh. Hỏi có bao nhiêu tam giác vuông có đỉnh là đỉnh của

Câu 3: (1,0 điểm)

Trong mặt phẳng tọa độ , cho điểm . Viết phương trình đường thẳng qua và cắt tia lần lượt tại sao cho tam giác có diện tích nhỏ nhất.

Câu 4: (0,5 điểm)

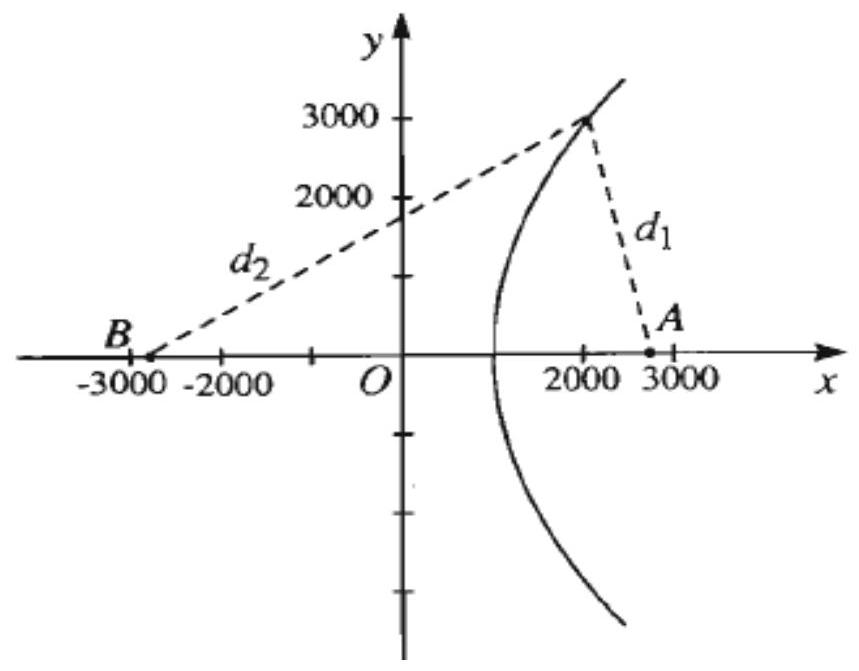
Hai thiết bị và dùng để ghi âm một vụ nổ đặt cách nhau 1 dặm, thiết bị ghi được âm thanh trước thiết bị là 2 giây, biết vận tốc âm thanh là 1100 feet / . Tìm các vị trí mà vụ nổ có thể xảy ra.

BÀI LÀM

…………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………………………………………………………

…………………………………………………………………………………………………

BÀI LÀM:

…………………………………………………………………………………………………

TRƯỜNG THCS ........

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 - 2023)

MÔN: TOÁN 10 - CÁNH DIỀU

A. PHẦN TRẮC NGHIỆM: (7,0 điểm)

Mỗi câu trả lời đúng được 0,25 điểm.

1.A	2.B	3.D	4.D	5.B	6.B	7.A	8.B	9.C	10. B
11.A	12.D	13.A	14.C	15.B	16.B	17.B	18.D	19.D	20. A
21.C	22.A	23.C	24.C	25.A	26.C	27.C	28.A

B. PHẦN TỰ LUẬN: (3,0 điểm)

Câu

Nội dung đáp án

Biểu điểm

Câu 1

(1,0 điểm)

Đặt

Gọi số tự nhiện lẻ có 6 chữa số là với thuộc và .

Vì nên .

+ Trường hợp 1:

có 3 cách chọn.

và có 4 cách chọn.

Mỗi bộ là một chỉnh hợp chập 4 của 8 phần tử còn lại thuộc tập có cách chọn.

Trường hợp này có số.

0,5

+ Trường hợp 2 :

có 2 cách chọn.

có 5 cách chọn.

Mỗi bộ là một chỉnh hợp chập 4 của 8 phần tử còn lại của tập có cách chọn.

Trường hợp này có số.

Vậy có tất cả số tự nhiên lẻ có 6 chữ số.

Gọi là biến cố bạn nhập một lần theo gợi ý của bác Bình mà đúng mật khẩu mở điện thoại.

Ta có . Vậy .

0,5

Câu 2

(0,5 điểm)

Đa giác đều có 48 đỉnh nên có 24 đường chéo đi qua tâm đường tròn ngoại tiếp đa giác đều .

Một tam giác vuông có đỉnh là đỉnh của thì phải có cạnh huyền là đường chéo đi qua tâm đường tròn ngoại tiếp đa giác đều . Với một đường chéo như vậy của đa giác đều sẽ tạo ra 46 tam giác vuông. Vậy số tam giác vuông có đỉnh là đỉnh của là tam giác vuông.

0,25

Câu 3.

(1,0 điểm)

Ta có phương trình đường thẳng có dạng: .

Do đi qua nên ta có .

Mặt khác diện tích của tam giác vuông là .

Áp dụng BĐT Cô si ta có:

0,5

Ta có diện tích của tam giác vuông nhỏ nhất bằng 32 khi thỏa mãn hệ phương trình: HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 - 2023) .

0,25

Vậy

HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 - 2023)

0,25

Câu 4

(0,5 điểm)

Chọn hệ trục tọa độ mà đi qua và là đường trung trực của .

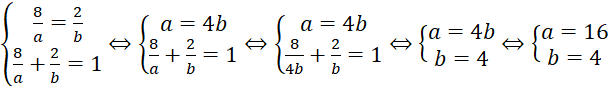
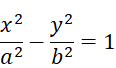
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KÌ 2 (2022 - 2023)

Kí hiệu là quãng đường âm thanh đi được từ vụ nổ đến thiết bị là quãng đường âm thanh đi được từ vụ nổ đến thiết bị và tính theo feet. Khi đó, do thiết bị nhận âm thanh nhanh hơn thiết bị là 2 giây nên ta có phương trình: