Tải giáo án powerpoint dạy thêm Toán 8 CTST Chương 3 Bài 5: Hình chữ nhật – Hình vuông

Nội dung giáo án

THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI  

BÀI HỌC MỚI 

BÀI 5:  

HÌNH CHỮ NHẬT – HÌNH VUÔNG 

PHIẾU BÀI TẬP SỐ 1 

DẠNG 1: Chứng minh tứ giác là hình chữ nhật, hình vuông 

Bài 1. Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB). Chứng minh PCQM là hình chữ nhật. 

Lời giải 

Ta có: A ̂=B ̂ (vì tam giác ABC vuông cân tại C) (1) 

Vì PM // BC nên (PMA) ̂=B ̂ (hai góc đồng vị) (2) 

Từ (1) và (2) suy ra A ̂=(PMA) ̂ (vì cùng bằng B ̂) 

⇒ ∆APM cân tại P ⇒ AP = PM (hai cạnh bên bằng nhau) 

Ta có: AP = CQ (gt) 

           AP = PM  

⇒ PM = CQ 

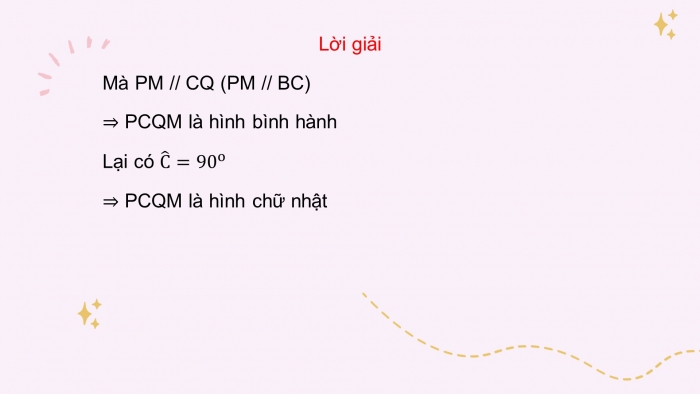
Mà PM // CQ (PM // BC) 

⇒ PCQM là hình bình hành 

Lại có C ̂=〖90〗^o 

⇒ PCQM là hình chữ nhật 

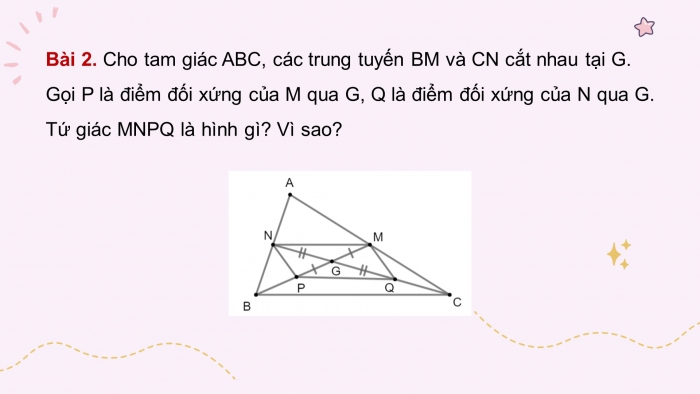
Bài 2. Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G, Q là điểm đối xứng của N qua G. Tứ giác MNPQ là hình gì? Vì sao? 

Lời giải 

∆ ABC cân tại A  

⇒ AC = AB (1) 

BM, CN là đường trung tuyến  

⇒ M, N lần lượt là trung điểm của AC, AB (2) 

⇒ AM = MC = AB/2;  

AN = NB = AC/2 (2) 

Từ (1) và (2) suy ra AM = MC = AN = NB 

Xét ∆ AMB và ∆ ANC có  

AB = AC 

A ̂ chung 

AM = AN 

⇒ ∆ AMB = ∆ ANC (g – c – g) ⇒ MB = NC  

Có P là điểm đối xứng của M qua G ⇒ GM = GP  

Q là điểm đối xứng của N qua G ⇒ GN = GQ 

 ⇒ MP = NQ 

Xét hình tứ giác MNPQ có 

GM = GP 

GN = GQ 

⇒ MNPQ là hình bình hành  

(vì G là trung điểm của hai đường chéo MN và PQ) 

Có MP = NQ nên MNPQ là hình chữ nhật 

Bài 3. Cho tam giác ABC vuông tại A, AD là đường phân giác. Kẻ đường cao DE (E ∈ AB), đường cao DF (F ∈ AC).  

Tứ giác AEDF là hình gì? Vì sao? 

Lời giải 

Xét tứ giác AEDF có A ̂=E ̂=F ̂=〖90〗^o 

⇒ AEDF là hình chữ nhật 

Mà AD là đường phân giác của góc A  

⇒ AEDF là hình vuông. 

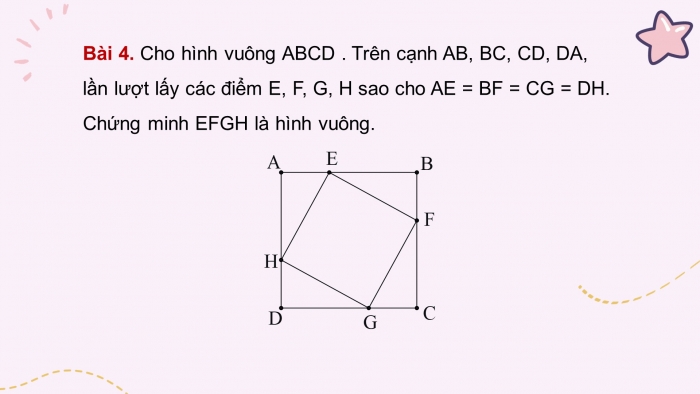
Bài 4. Cho hình vuông ABCD . Trên cạnh AB, BC, CD, DA, lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Chứng minh EFGH là hình vuông. 

Lời giải 

Vì ABCD là hình vuông ⇒ AB = BC = DC = AD 

Có AE = BF = CG = DH 

⇒ AH = BE = CF = DG (1) 

Xét ∆AEH và ∆BFE có 

AE = BF (gt) 

A ̂ = B ̂ (= 90o) 

AH = BE (cmt) 

⇒ ∆AEH = ∆BFE (c – g – c) ⇒ EH = FE 

Tương tự ∆AEH = ∆CGF (c – g – c) ⇒ EH = GF 

                ∆AEH = ∆DHG (c – g – c) ⇒ EH = HG 

⇒ EH = FE = GF = HG 

Mặt khác, vì ∆AEH = ∆BFE ⇒ (AHE) ̂ = (BEF) ̂ 

Suy ra (AHE) ̂ + (BEF) ̂ = 90o ⇒ (FEH) ̂ = 90o (2). 

Từ (1), (2) suy ra EFGH là hình vuông. 

PHIẾU BÀI TẬP SỐ 2 

DẠNG 2: Vận dung tính chất của  

hình chữ nhật, hình vuông để  

chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng 

Bài 1. Cho hình chữ nhật ABCD, AB = 40 cm, AD = 30 cm, O là giao điểm của hai đường chéo, AO = 25 cm. Gọi H là chân đường vuông góc kẻ từ A đến BD. Tính độ dài đoạn DH, OH, OB. 

Lời giải 

Áp dụng định lí Pythagore vào ∆ABC có  

BC^2=AB^2+AC^2=〖40〗^2+〖30〗^2=2500=〖50〗^2⇒BC=50 cm  

Vì ABCD là hình chữ nhật nên OA = OB = OC = OD= 25 cm 

 Áp dụng định lí Pythagore vào ∆ADH có 

 AD^2=DH^2+AH^2⇒AH^2=AD^2-DH^2 (1) 

Áp dụng định lí Pythagore vào ∆AOH có 

 AO^2=OH^2+AH^2⇒AH^2=AO^2-OH^2=AO^2-(OD-DH)^2 (2) 

Từ (1) và (2) ta được 

AD^2-DH^2= AO^2-(OD-DH)^2  

⇒〖30〗^2-DH^2=〖25〗^2-(〖25〗^2-DH^2 )  

⇔900-DH^2=625-625+50DH-DH^2  

⇔50DH=900  

⇔DH=18 cm  

⇒HO=25-18=7 cm 

Bài 2. Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo, điểm E thuộc cạnh CD. Đường vuông góc với AE tại A cắt BC ở F.  

Gọi M là trung điểm của EF.  

Chứng minh rằng OM là đường trung trực của AC. 

Lời giải 

Gọi O là giao điểm của hai đường chéo của hình chữ nhật ABCD nên OA = OC (1) 

Xét ∆AEF vuông tại A có AM là đường trung tuyến 

⇒ AM = EM = MF 

Xét ∆CEF vuông tại C có CM là đường trung tuyến 

⇒ CM = EM = MF 

⇒ AM = CM (2) 

Từ (1) và (2) suy ra OM là đường trung trực của AC. 

Bài 3. Cho hình vuông ABCD, trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN và AM ⊥ BN. 

Lời giải 

Xét ∆ABM và ∆BCN có 

       AB = BC ( ABCD là hình vuông) 

       (ABM) ̂ = (BCN) ̂ (ABCD là hình vuông) 

       BM = CN (gt) 

⇒ ∆ABM = ∆BCN (c.g.c) ⇒ AM = BN 

⇒ (BAM) ̂=(CBN) ̂ 

Có (ABN) ̂+(CBN) ̂=(ABC) ̂=〖90〗^o 

⇒ (BAM) ̂+(ABN) ̂=〖90〗^o 

Gọi I là giao điểm của AM và BN 

Xét tam giác ABI có  

(BAI) ̂+(ABI) ̂+(AIB) ̂=〖180〗^o 

⇒(AIB) ̂=〖180〗^o-((BAI) ̂+(ABI) ̂ )=〖180〗^o-〖90〗^o=〖90〗^o  

⇒ AM ⊥ BN 

Bài 4. Cho hình vuông ABCD cạnh a. Trên hai cạnh BC, CD lấy  

hai điểm M, N sao cho (MAN) ̂=〖45〗^o, trên tia đối của tia DC lấy điểm K sao cho DK = BM. Hãy tính: 

1. a) Số đo góc KAN
2. b) Chu vi tam giác MCN theo a

...