Tải giáo án powerpoint dạy thêm Toán 8 CTST Chương 3 Bài 4: Hình bình hành – Hình thoi

Nội dung giáo án

KÍNH CHÀO QUÝ THẦY CÔ VÀ CÁC BẠN ĐẾN VỚI BUỔI HỌC HÔM NAY 

BÀI 4:  

HÌNH BÌNH HÀNH – HÌNH THOI 

DẠNG 1: Chứng minh tứ giác là hình bình hành, hình thoi 

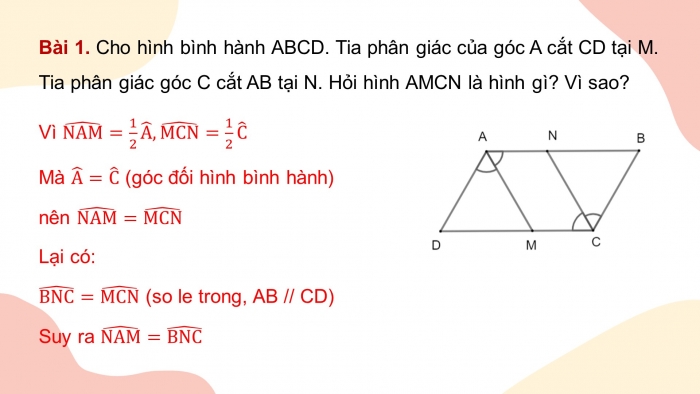
Bài 1. Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M. Tia phân giác góc C cắt AB tại N. Hỏi hình AMCN là hình gì? Vì sao? 

Vì (NAM) ̂=1/2 A ̂, (MCN) ̂=1/2 C ̂ 

Mà A ̂=C ̂ (góc đối hình bình hành) 

nên (NAM) ̂=(MCN) ̂ 

Lại có: 

(BNC) ̂=(MCN) ̂ (so le trong, AB // CD) 

Suy ra (NAM) ̂=(BNC) ̂ 

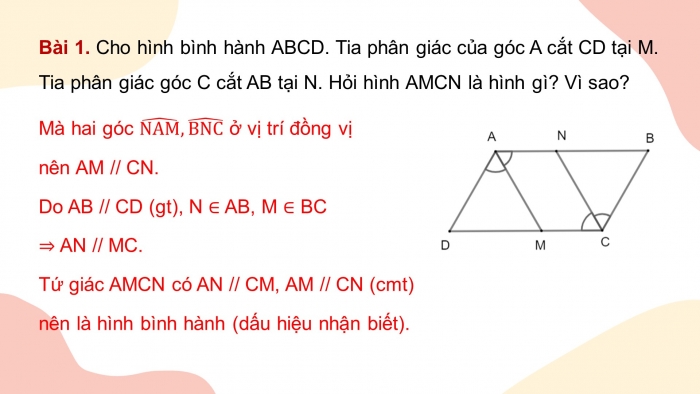
Mà hai góc (NAM) ̂, (BNC) ̂ ở vị trí đồng vị  

nên AM // CN. 

Do AB // CD (gt), N ∈ AB, M ∈ BC  

⇒ AN // MC. 

Tứ giác AMCN có AN // CM, AM // CN (cmt)  

nên là hình bình hành (dấu hiệu nhận biết). 

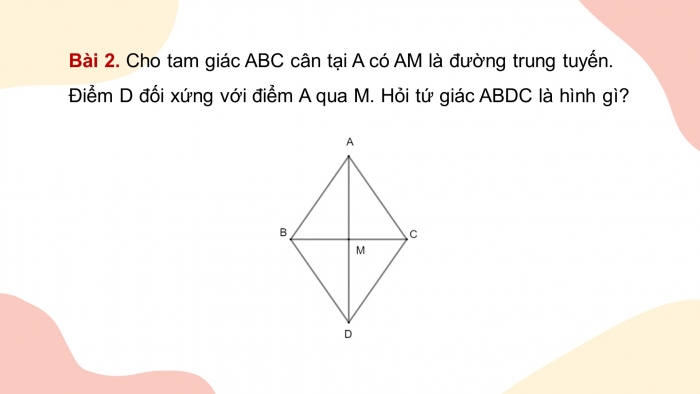
Bài 2. Cho tam giác ABC cân tại A có AM là đường trung tuyến. Điểm D đối xứng với điểm A qua M. Hỏi tứ giác ABDC là hình gì? 

Lời giải 

Do tam giác ABC cân tại A có AM là đường trung tuyến nên đồng thời là đường cao: 

AM ⊥ BC và M là trung điểm của BC. 

Do D đối xứng với A qua M nên M là trung điểm của AD. 

Tứ giác ABDC có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành. 

Lại có: AD ⊥ BC nên tứ giác ABDC là hình thoi. 

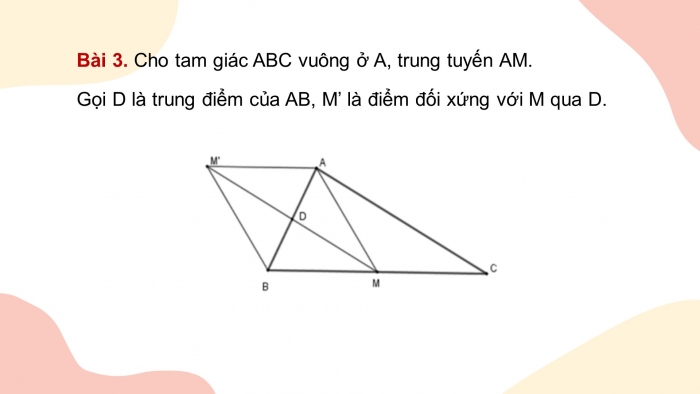
Bài 3. Cho tam giác ABC vuông ở A, trung tuyến AM.  

Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. 

Vì M’ đối xứng M qua D nên DM = DM’ (1) 

M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình  

của ΔABC. 

Suy ra MD // AC (2) 

Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2) 

Từ (1) và (2) suy ra DM ⊥ AB ⇒ MM’ ⊥ AB. 

Vì D là trung điểm của AB (gt) và D là trung điểm của MM’ nên  

tứ giác AMBM’ là hình bình hành.  

Mặt khác MM’ ⊥ AB nên AMBM’ là hình thoi. 

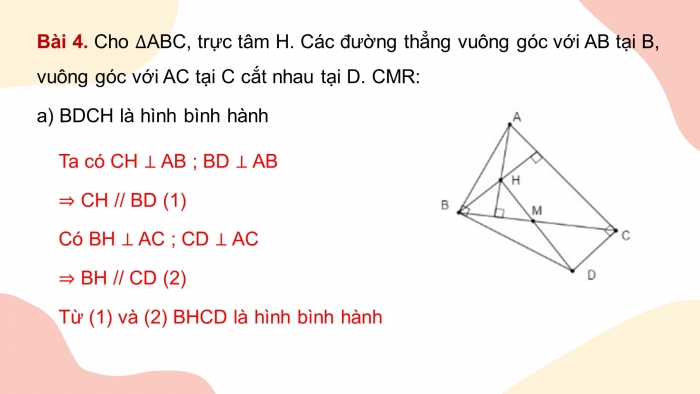
Bài 4. Cho ∆ABC, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. CMR: 

1. a) BDCH là hình bình hành

Ta có CH ⊥ AB ; BD ⊥ AB 

⇒ CH // BD (1) 

Có BH ⊥ AC ; CD ⊥ AC 

⇒ BH // CD (2) 

Từ (1) và (2) BHCD là hình bình hành 

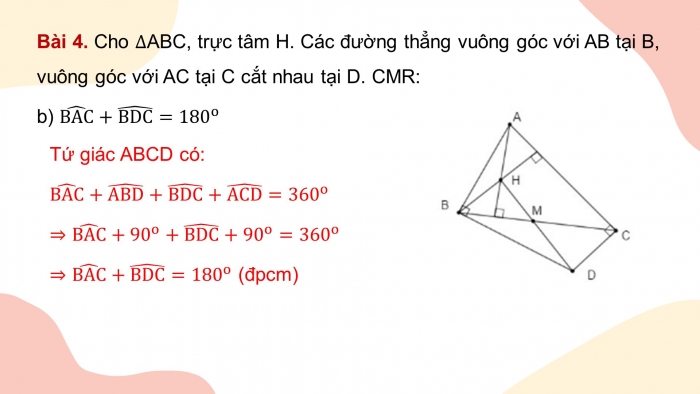
1. b) (BAC) ̂+(BDC) ̂=〖180〗^o

Tứ giác ABCD có:  

(BAC) ̂+(ABD) ̂+(BDC) ̂+(ACD) ̂=〖360〗^o  

⇒(BAC) ̂+〖90〗^o+(BDC) ̂+〖90〗^o=〖360〗^o  

⇒(BAC) ̂+(BDC) ̂=〖180〗^o (đpcm) 

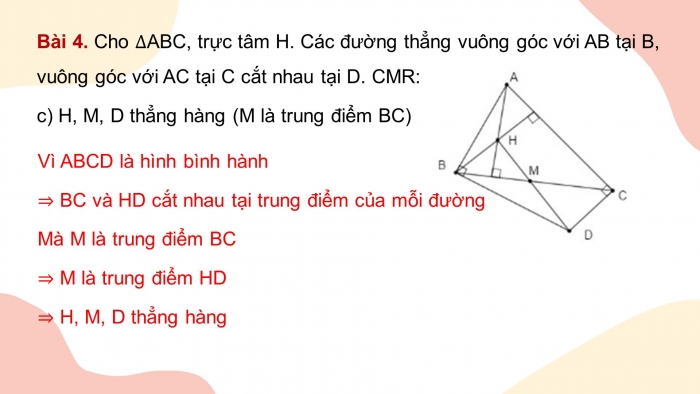
1. c) H, M, D thẳng hàng (M là trung điểm BC)

Vì ABCD là hình bình hành  

⇒ BC và HD cắt nhau tại trung điểm của mỗi đường 

Mà M là trung điểm BC 

⇒ M là trung điểm HD 

⇒ H, M, D thẳng hàng 

PHIẾU BÀI TẬP SỐ 2 

DẠNG 2: Vận dụng tính chất của  

hình bình hành, hình thoi để  

chứng minh các tính chất hình học 

Bài 1. Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD. 

1. a) Chứng minh rằng AF // CE
2. b) Gọi M, N theo thứ tự là giao điểm của BD với AF, CE.

Chứng minh rằng DM = MN = NB 

Lời giải 

1. a) Ta có ABCD là hình bình hành nên AB = CD (tc hbh)

Mà E, F là trung điểm của AB và CD 

⇒ AB = CF = BE = DF 

Xét tứ giác AECF có 

AE = CF 

AE // CF ( do AB // CD) 

⇒ AECF là hình bình hành ⇒ AF // EC 

1. b) Gọi AC ∩ BD = {O}

Xét ∆ADC có DO, AF là trung tuyến; AF ∩ DO = {M} 

⇒ M là trọng tâm của ∆ADC  

⇒ DM = 2/3 DO = 2/3 BO (1) 

     OM = 1/3 DO = 1/3 BO (2) 

Xét ∆ABC có BO, CE là trung tuyến; BO ∩ CE = {N} 

⇒ N là trọng tâm của ∆ABC  

⇒ BN =  2/3 BO (3) 

     ON = 1/3 BO (4) 

Từ (2) và (4) ⇒ MN = OM + ON = 1/3 BO + 1/3 BO = 2/3 BO (5) 

Từ (1), (3) và (5) ⇒ DM = BN = MN (đpcm). 

Bài 2. Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Trên cạnh AB, BC, CD, DA lấy theo thứ tự các điểm M, N, P, Q  

sao cho AM = CN = CP = AQ. Chứng minh M, O, P thẳng hàng  

và N, O, Q thẳng hàng 

Lời giải 

+) Vì ABCD là hình thoi ⇒ AB // CD ⇒ MB // DP (1) 

Lại có: AB = DC (ABCD là hình thoi) 

Mà AM = CP (gt) 

⇒ MB = DP (2) 

Từ (1) và (2) ⇒ MBPD là hình bình hành 

⇒ BD và MP cắt nhau tại trung điểm của mỗi đường 

Mà O là trung điểm BD 

⇒ O là trung điểm MP ⇒ M, O, P thẳng hàng 

+) Vì ABCD là hình thoi ⇒ AD // BC ⇒ BN // QD (3) 

Lại có: AD = BC (ABCD là hình thoi) 

Mà AQ = CN (gt) 

⇒ DQ = ND (4) 

Từ (3) và (4) ⇒ BNDQ là hình bình hành 

⇒ BD và NQ cắt nhau tại trung điểm của mỗi đường 

Mà O là trung điểm BD 

⇒ O là trung điểm NQ ⇒ N, O, Q thẳng hàng 

Bài 3. Cho tam giác nhọn ABC. Vẽ phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE. Chứng minh hai đường thẳng MA và BC vuông góc với nhau. 

...