Soạn giáo án điện tử Toán 8 CTST Chương 3 Bài 2: Tứ giác

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

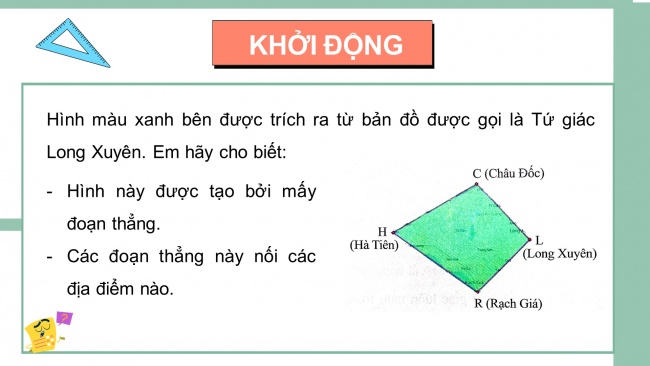
Hình màu xanh bên được trích ra từ bản đồ được gọi là Tứ giác Long Xuyên. Em hãy cho biết:

• Hình này được tạo bởi mấy đoạn thẳng.
• Các đoạn thẳng này nối các địa điểm nào.

CHƯƠNG 3. ĐỊNH LÝ PYTHAGORE.

CÁC LOẠI TỨ GIÁC THƯỜNG GẶP

BÀI 2. TỨ GIÁC

NỘI DUNG BÀI HỌC

Tứ giác

Tổng các góc của một tứ giác

1. TỨ GIÁC

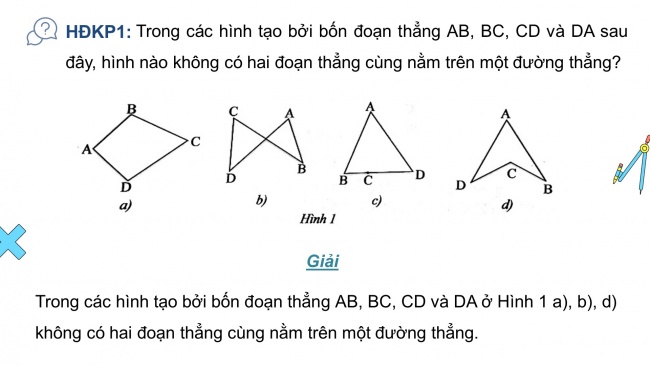
                  Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?

Giải

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1 a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.

KẾT LUẬN

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

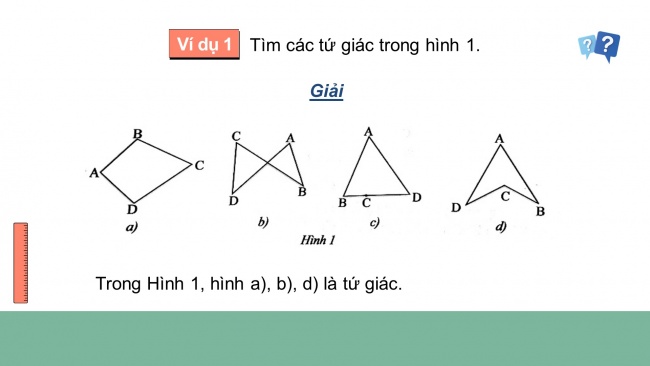
Ví dụ 1

Tìm các tứ giác trong hình 1.

Giải

Trong Hình1, hình a), b), d) là tứ giác.

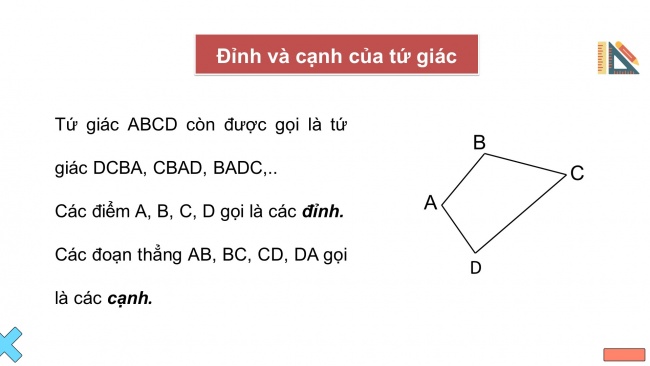
Đỉnh và cạnh của tứ giác

Tứ giác ABCD còn được gọi là tứ giác DCBA, CBAD, BADC,..

Các điểm A, B, C, D gọi là các đỉnh.

Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh.

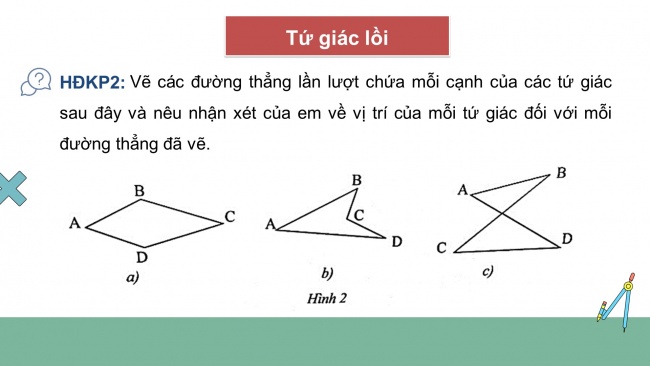
Tứ giác lồi

                  Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.

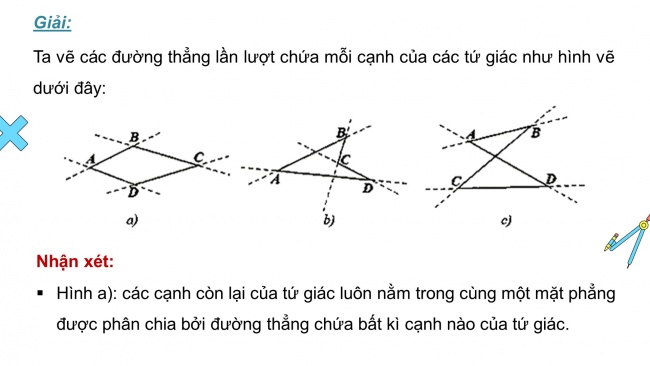
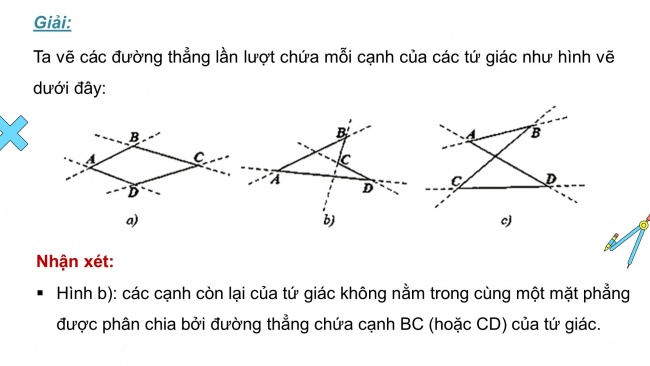
Giải:

Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:

Nhận xét:

• Hình a): các cạnh còn lại của tứ giác luôn nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.
• Hình b): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.
• Hình c): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.

KẾT LUẬN

Tứ giác lồi là tứ giác luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

Ví dụ 2

Tìm tứ giác lồi trong các hình sau

         Kẻ các đường thẳng chứa mỗi cạnh của tứ giác như hình dưới, ta thấy ABCD là tứ giác lồi còn EFGH không phải là tứ giác lồi.

Chú ý:

Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.

Cạnh, góc, đường chéo của tứ giác

Trong một tứ giác:

1. a) Hai cạnh kề nhau là hai cạnh có chung một đỉnh.

VD: Trong hình 5, BA và BC là hai cạnh kề nhau.

1. b) Hai cạnh kề nhau tạo thành một góc của tứ giác.

VD: Trong hình 5, tứ giác ABCD có các góc là . Các cặp góc  và ;  và  được cặp góc đối.

1. c) Hai cạnh đối nhau là hai cạnh không có chung đỉnh nào.

VD: Trong hình 5, AB và DC là hai cạnh đối nhau.

1. d) Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.

VD: Trong hình 5, A và C là hai đỉnh đối nhau.

1. e) Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.

VD: Trong hình 5, tứ giác ABCD có hai đường chéo là AC và BD.

Thực hành 1

Vẽ tứ giác MNPQ và tìm:

• Hai đỉnh đối nhau;
• Hai đường chéo;
• Hai cạnh đối nhau.

Giải:

Trong tứ giác MNPQ có:

• Hai đỉnh đối nhau: M và P; N và Q;
• Hai đường chéo: MP và NQ;
• Hai cạnh đối nhau: MN và PQ; MQ và NP.

Vận dụng 1

Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).

Giải

Trong tứ giác Long Xuyên CHRL có:

• Các đỉnh: C, H, R, L;
• Các cạnh: CH, HR, RL, LC;
• Các đường chéo: CR và HL.

2. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC

                  Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

Giải

Xét tam giác ACB có:

 (định lí tổng ba góc trong một tam giác).

Xét tam giác ACD có:

 (định lí tổng ba góc trong một tam giác).

Do

Suy ra  

Hay

Vậy tổng các góc của tứ giác ABCD bằng

KẾT LUẬN

Tổng số đo các góc của một tứ giác bằng .

Ví dụ 3

Tìm số đo x ở mỗi tứ giác sau

Giải

--------------- Còn tiếp ---------------