a) Vẽ $\widehat{xOy}$ có số đo là $120^{\circ}$
Bài 3.
a) Vẽ $\widehat{xOy}$ có số đo là $120^{\circ}$
b) Vẽ tia phân giác của $\widehat{xOy}$ trong câu a
a) Để vẽ $\widehat{xOy}$ có số đo là $120^{\circ}$ ta làm như sau:
- Vẽ tia Ox: 
- Đặt thước đo góc sao cho tâm của thước trùng với O, vạch 0 của thước nằm trên tia Ox.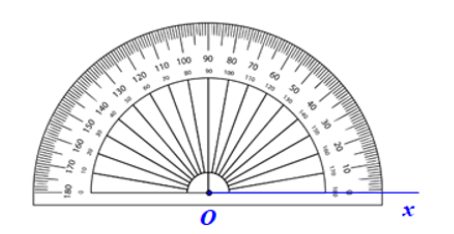
- Đánh dấu một điểm trên vạch chia độ của thước tương ứng với số chỉ $120^{\circ}$, kẻ tia Oy đi qua điểm đã đánh dấu.
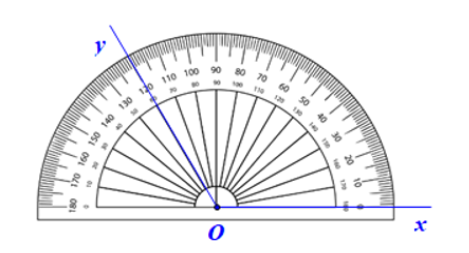
Ta có $\widehat{xOy}=120^{\circ}$ đã được vẽ.
b) - Vẽ tia phân giác của $\widehat{xOy}=120^{\circ}$ bằng cách dùng thước đo góc.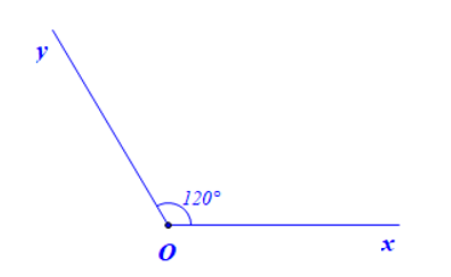
- Ta có: $\widehat{xOz}=\widehat{yOz}$ và $\widehat{xOz}+\widehat{yOz}=120$
Suy ra $\widehat{xOz}==60$
- Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của $\widehat{xOy}$ sao cho $\widehat{xOz}=60$
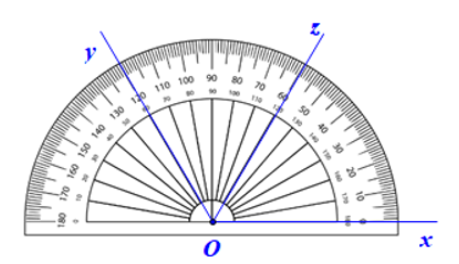
- Ta được tia Oz là tia phân giác của $\widehat{xOy}$
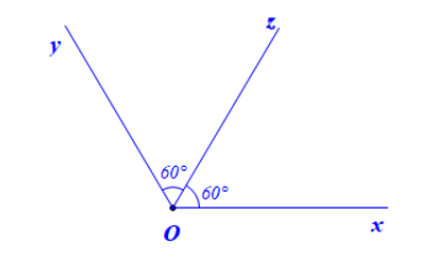
- Ngoài cách vẽ trên ta có thể vẽ tia phân giác của $\widehat{xOy}=120^{\circ}$ bằng cách dùng thước thẳng và compa.
- Vẽ cung tròn tâm O cắt Ox và Oy lần lượt tại M và N
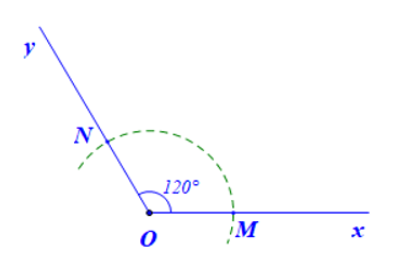 -
-
- Vẽ hai cung tròn có bán kính bằng nhau, có tâm lần lượt tại M, N và cắt nhau tại một điểm P bên trong góc xOy.
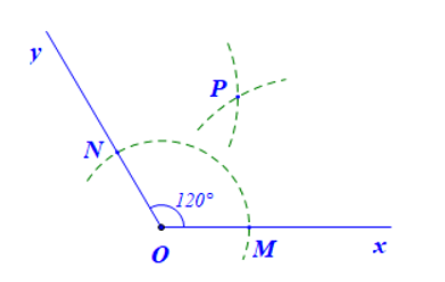
- Vẽ tia OP ta được phân giác góc xOy.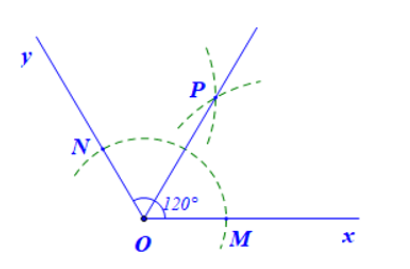
Xem toàn bộ: Giải SBT toán 7 Chân trời bài 2 Tia phân giác

Bình luận