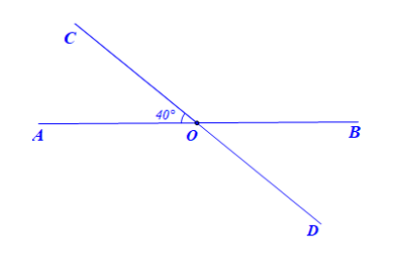
Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành $\widehat{AOC}=40^{\circ}$
Bài 4. Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành $\widehat{AOC}=40^{\circ}$
a) Tính số đo các góc còn lại.
b) Vẽ Ox là tia phân giác của $\widehat{AOC}$. Hãy tính số đo của $\widehat{xOD}$ và $\widehat{xOB}$
c) Vẽ Oy là tia đối của tia Ox. Chứng tỏ rằng Oy là tia phân giác của $\widehat{BOD}$
a) $\widehat{BOD}=\widehat{AOC}= 40^{\circ}; \widehat{COB}=\widehat{AOD}=140^{\circ}$
b) $\widehat{xOB}=\widehat{xOD}=20^{\circ}+140^{\circ}=160^{\circ}$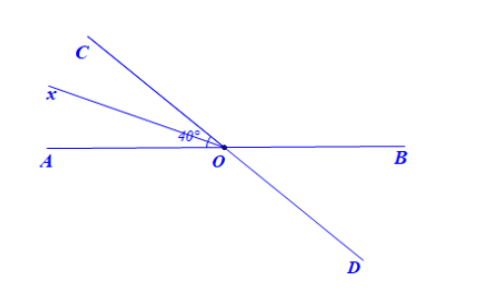 
c) Ta có: $\widehat{yOB}=\widehat{xOA}$ (đối đỉnh), $\widehat{yOD}=\widehat{xOC}$ (đối đỉnh), $\widehat{xOA}=\widehat{xOC}$(giả thiết)
Suy ra $\widehat{yOB}=\widehat{yOD}$.
Vậy Oy là tia phân giác của $\widehat{BOD}$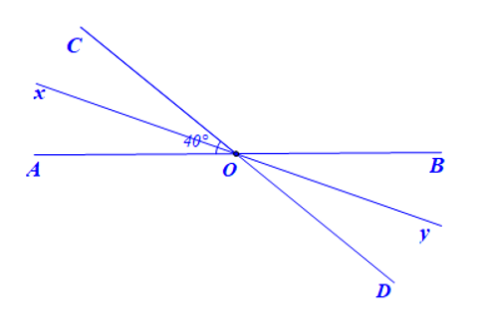
Xem toàn bộ: Giải SBT toán 7 Chân trời bài 2 Tia phân giác
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận