Vẽ hai góc kề bù $\widehat{xOy},\widehat{yOz}$, biết $\widehat{xOy}=130^{\circ}$.
Bài 5. Vẽ hai góc kề bù $\widehat{xOy},\widehat{yOz}$, biết $\widehat{xOy}=130^{\circ}$. Gọi Ot là tia phân giác của $\widehat{xOY}$. Tính $\widehat{tOz}$
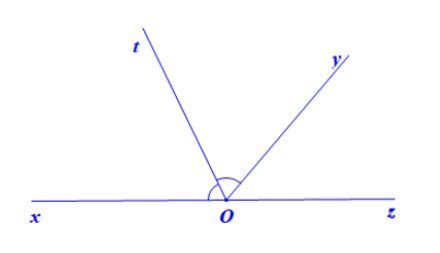
Vì Ot là tia phân giác của $\widehat{xOy}$ nên:
$\widehat{xOt}=\widehat{tOy}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}130^{\circ}=65^{\circ}$
Vì $\widehat{xOt}$ và $\widehat{tOz}$ là hai góc kề bù nên ta có:
$ \widehat{xOt}+\widehat{tOz}=180^{\circ}$
Suy ra $\widehat{tOz}=180^{\circ}-\widehat{xOt}=180^{\circ}-65^{\circ}=115^{\circ}$
Vậy $\widehat{tOz}=115^{\circ}$
Xem toàn bộ: Giải SBT toán 7 Chân trời bài 2 Tia phân giác
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận