Một con lắc lò xo gồm vật nhỏ có khối lượng m = 0,03 kg và lò xo có độ cứng k = 1,5 N/m. Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục của lò xo...

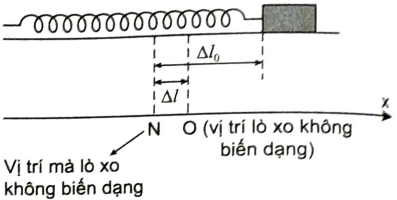
Vật đạt tốc độ lớn nhất tại vị trí O mà lực ma sát cân bằng với lực đàn hồi của lò xo, khi đó vật còn cách vị trí mà lò xo không biến dạng một đoạn A xác định bởi

$\mu mg=k.\Delta l\Rightarrow\Delta l=\frac{\mu.mg}{k}= \frac{0,2.0,03.10}{1,5} =0,04$ m.

Công của lực ma sát trên đoạn $\Delta l_{0}-\Delta l$ đó bằng độ giảm cơ năng khi vật đi từ vị trí ban đầu tới vị trí cân bằng nói trên:

$\mu mg(\Delta l_{0} – \Delta l) = \frac{mv_{max}^{2}}{2}+ \frac{k \Delta l^{2}}{2}-\frac{k.\Delta l_{0}^{2}}{2}$.

Thay số: $-0,1.0,03.10(0, 15 - 0,04) = \frac{0,03v^{2}_{max}}{2}+\frac{1,5.0,04^{2}}{2} - \frac{1,5.0,15^{2}}{2}$

Suy ra: $v_{max} =0,91 m/s=91 cm/s$.