Giải luyện tập 1 trang 110 sgk Toán 8 tập 1 CD
Luyện tập 1 trang 110 sgk Toán 8 tập 1 CD: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M,N lần lược là hình chiếu của O trên AB, BC. Chứng minh MN = $\frac{1}{2}$ AC.
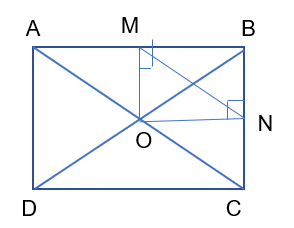
Tứ giác MBNO có 3 góc vuông là OMB, MBN và ONB nên góc còn lại là NOM cũng là góc vuông. Vậy MBNO là hình chữ nhật.
=> MO = BN (1)
MO//BN (hay MO//CN) (2)
N là hình chiếu của O trên BC nên NB=NC (3)
Từ (1) và (3) => MO = NC. kết hợp với (2) suy ra OMNC là hình bình hành (tứ giác cócặp cạnh đối song song và bằng nhau)
=> MN = OC. Mà O là giao điểm 2 đường chéo của hình chữ nhật ABCD nên OC= $\frac{1}{2}$ AC. Vậy MN = $\frac{1}{2}$ AC (đpcm)
Xem toàn bộ: Giải toán 8 cánh diều bài 5 Hình chữ nhật

Bình luận