Giải Câu 9 Bài: Ôn tập cuối năm sgk Hình học 10 Trang 99
Câu 9: Trang 99 - SGK Hình học 10
Cho elip \((E)\) có phương trình: \({{{x^2}} \over {100}} + {{{y^2}} \over {36}} = 1\)
a) Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip \((E)\) và vẽ elip đó
b) Qua tiêu điểm của elip dựng đường thẳng song song với \(Oy\) và cắt elip tại hai điểm \(M\) và \(N\). Tính độ dài đoạn thẳng \(MN\).
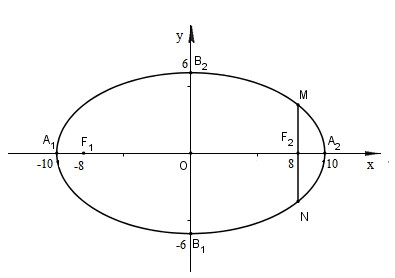
a) Từ phương trình của elip, ta có:
\(a^2= 100 ⇒ a = 10\)
\(b^2= 36 ⇒ b = 6\)
\(c^2= a^2– b^2= 64 ⇒ c = 8\)
Từ đó ta có tọa độ các đỉnh của elip là: \(A_1(-10; 0), A_2(10; 0), B_1(0; -3), B_2(0;3)\)
và tọa độ tiêu điểm là: \(F_1(-8; 0), F_2(8; 0)\)
b) Đường thẳng MN song song với Oy và đi qua tiêu điểm $F_2$ của elip nên hoành độ của M, N cũng chính là hoành độ của tiêu điểm.
=> Hoành độ của M, N là $x=8$.
Thế \(x = 8\) vào phương trình của elip ta được:
\({{64} \over {100}} + {{{y^2}} \over {36}} = 1 \Rightarrow y = \pm {{18} \over 5}\)
=> Ta có: $M(8;\frac{18}{5});N(8;\frac{-18}{5})$
\(\Rightarrow \vec {MN} = (0;\frac{36}{5})\Rightarrow MN={{36} \over 5}\)
Xem toàn bộ: Giải Bài: Ôn tập cuối năm sgk Hình học 10 Trang 98

Bình luận