Giải Bài tập 4.9 trang 83 sgk Toán 8 tập 1 Kết nối
Bài tập 4.9 trang 83 sgk Toán 8 tập 1 KNTT: Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh rằng tứ giác AHOK là hình chữ nhật
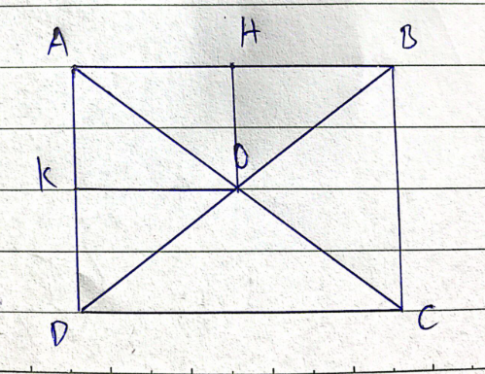
Ta có: OA = OB suy ra tam giác OAB cân tại B, OH là đường trung tuyến nên OH cũng là đường cao, do đó $\widehat{OHA}=90^{\circ}$
Tương tự, $\widehat{OKA}=90^{\circ}$
Xét tứ giác AHOK có: $\widehat{A}=\widehat{OKA}=\widehat{OHA}=90^{\circ}$ suy ra AHOK là hình chữ nhật

Bình luận