Giải Bài tập 3.5 trang 55 sgk Toán 8 tập 1 Kết nối

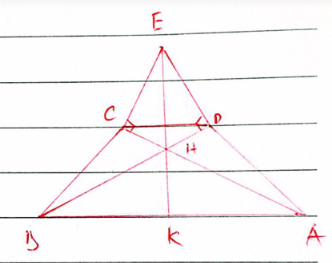
Gọi giao điểm của AC và BD là H

Xét tam giác vuông ECH và EDH, ta có:

EH chung

EC = ED (gt)

Suy ra $\Delta ECH=\Delta EDH$ (cạnh huyền - cạnh góc vuông) $\Rightarrow CH = DH$ (1)

Ta có $\widehat{CEH}=\widehat{DEH}$ (do $\Delta ECH=\Delta EDH$ ) suy ra EH là tia phân giác của tam giác cân ECD $\Rightarrow EH\perp CD\Rightarrow  EH\perp AB$ (do AB//CD)

Gọi giao điểm của EH và AB là K

$\Delta ECH=\Delta EDH\Rightarrow \widehat{EHC}=\widehat{EHD}\Rightarrow \widehat{BHK}=\widehat{AHK}$

Xét tam giác vuông BHK và AHK ta có:

HK chung

$\widehat{BHK}=\widehat{AHK}$

Suy ra $\Delta BHK=\Delta AHK$ (cạnh góc vuông - góc nhọn kề) $\Rightarrow BH = AH$ (2)

Từ (1) và (2) suy ra AC = BD $\Rightarrow $hình thang ABCD là hình thang cân