Giải Bài tập 3.35 trang 73 sgk Toán 8 tập 1 Kết nối

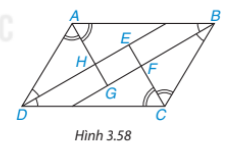
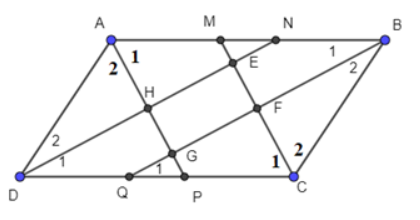
Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình bình hành.

Ta có: $\widehat{D1}=\widehat{D2}=\frac{\widehat{ADC}}{2}$(DN là phân giác $\widehat{ADC}$)

$\widehat{B1}=\widehat{B2}=\frac{\widehat{ABC}}{2}$(BQ là phân giác $\widehat{ABC}$)

Mà $\widehat{ABC}=\widehat{ADC}$ (hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{D1}=\widehat{B1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{Q1}=\widehat{B1}$ (hai góc so le trong)

$\Rightarrow \widehat{D1}=\widehat{B1}$

Mà hai góc ở vị trí đồng vị

⇒DN // BQ hay HE // GF

Ta có: $\widehat{A1}=\widehat{A2}=\frac{\widehat{DAB}}{2}$ (AP là phân giác $\widehat{DAB}$)

$\widehat{C1}=\widehat{C2}=\frac{\widehat{DCB}}{2}$(CM là phân giác$\widehat{DCB}$)

Mà $\widehat{DAB}=\widehat{DCB}$ (hai góc đối của hình bình hành ABCD)

$\Rightarrow \widehat{A1}=\widehat{C1}$

Vì ABCD là hình bình hành AB // CD $\Rightarrow \widehat{A1}=\widehat{QPG}$ (hai góc so le trong)

$\Rightarrow \widehat{C1}=\widehat{QPG}$

⇒AP //DM hay GH // EF

Xét tứ giác EFGH có:

HE // GF (cmt)

GH // EF (cmt)

⇒EFGH là hình bình hành (1)

Xét tam giác BFC, có:

$\widehat{B2}+\widehat{C2}=\frac{\widehat{ABC}}{2}+\frac{\widehat{BCD}}{2}=\frac{\widehat{ABC}+\widehat{BCD}}{2}$

Mà $\widehat{ABC}+\widehat{BCD}=180$(hai góc trong cùng phía bù nhau)

$\Rightarrow \widehat{B2}+\widehat{C2}=\frac{180^{\circ}}{2}=90^{\circ}$

$\Rightarrow \widehat{BFC}=180^{\circ}-(\widehat{B2}+\widehat{C2})=90^{\circ}$ hay $\Rightarrow \widehat{EFG}=90^{\circ}$

Từ (1) và (2) suy ra tứ giác EFGH là hình chữ nhật.