Giải Bài tập 3.32 trang 72 sgk Toán 8 tập 1 Kết nối

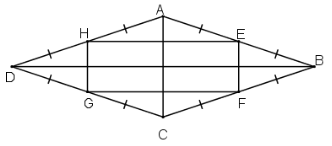
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC

=> EF là đường trung bình của tam giác ABC

$\Rightarrow EF//AC$ và $EF=\frac{AC}{2}$ (1)

* Tương tự tam giác ADC có HG là đường trung bình nên:

HG // AC và $HG=\frac{AC}{2}$ (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

=> tứ giác EFGH là hình bình hành.

Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH

Nên $\widehat{FEH}=90^{\circ}$

Hình bình hành EFGH có $\widehat{E}=90^{\circ}$ nên là hình chữ nhật