Giải Bài tập 3.12 trang 56 sgk Toán 8 tập 1 Kết nối
Bài tập 3.12 trang 56 sgk Toán 8 tập 1 KNTT: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R
a) Chứng minh tứ giác APMR là hình thang cân
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
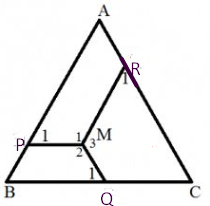
a) Ta có MR // AP suy ra APMR là hình thang
PM // BQ suy ra $\widehat{P1}=\widehat{B}$ (hai góc đồng vị)
Lại có: $\widehat{A}=\widehat{B}$ (do tam giác ABC đều) $\Rightarrow \widehat{A}=\widehat{P1}$
Suy ra APMR là hình thang cân
b) Tương tự câu a) ta chứng minh được tứ giác QMRC và PMQB là hình thang cân
suy ra PR = MA, RQ = MC, PQ = MB (cặp đường chéo của hình thang cân)
$\Rightarrow PR+RQ+PQ=MA+MB+MC$
c) Tam giác PRQ đều khi PR = RQ = PQ hay MA = MB = MC suy ra M cách đều 3 đỉnh tam giác ABC hay chính là tâm đương tròn ngoại tiếp tam giác ABC
Xem toàn bộ: Giải toán 8 kết nối bài Luyện tập chung trang 56

Bình luận