Giải bài 9 trang 35 SBT toán 10 tập 1 chân trời
Bài 9 : Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu đồng. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 8 triệu đồng. Hãy lập kế hoạch sản xuất cho xưởng nói trên sao cho có tổng số tiền lãi cao nhất.
Gọi x và y lần lượt là số tấn sản phẩm X và Y mà xưởng cần sản xuất (x ≥ 0, y ≥ 0).
Ta có hệ bất phương trình sau:
$\left\{\begin{matrix}3x+y ≤ 6 & & \\ x+y ≤ 4 & & \\ x ≤ 0 & & \\ y ≤ 0 & & \end{matrix}\right.$
Biểu diễn miền nghiệm của hệ bất phương trình ta được miền tứ giác OABC có tọa độ các đỉnh là: O(0; 0), A(0; 4), B(1; 3), C(2; 0) (Hình 2)
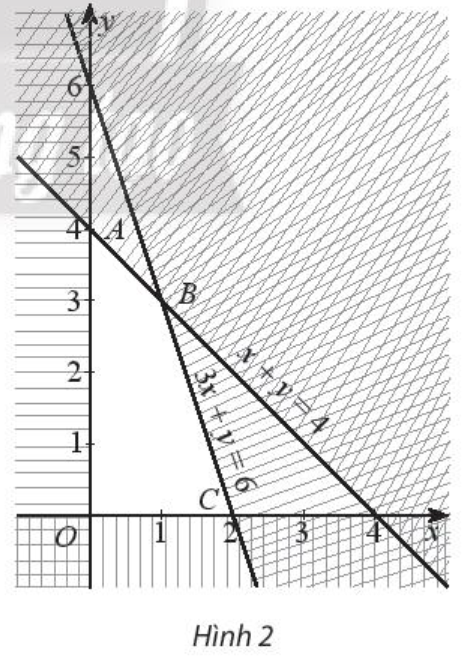
Số tiền lãi F = 10x + 8y đạt GTLN là 34 triệu đồng tại đỉnh B(1; 3).
Vậy xưởng cần sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y thì sẽ có tổng tiền lãi cao nhất.

Bình luận