Giải bài 6.19 bài dấu của tam thức bậc hai
Bài tập 6.19. Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x. Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
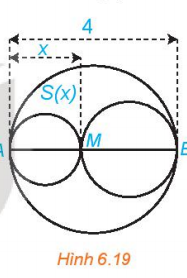
- AM = x, AB = 4 => MB = 4 -x, nên bán kính đường tròn đường kính AM là $\frac{x}{2}$ , bán kính đường tròn đường kính MB là $\frac{4-x}{2}$.
- Diện tích hình tròn đường kính AM là: $S_{1}=\pi \frac{x^{2}}{4}$.
Diện tích hình tròn đường kính MB là: $S_{2}=\pi \frac{(4-x)^{2}}{4}$.
Diện tích hình tròn đường kính AB là: $S=\pi .16$.
- Diện tích S(x) = $\pi .16- \pi \frac{x^{2}}{4}-\pi \frac{(4-x)^{2}}{4}$ = $\pi \frac{-2x^{2}+8x+48}{4}$
- Theo đề bài $S(x) \leq \frac{1}{2}(S_{1}+S_{2})$
$\Leftrightarrow $ $\pi \frac{-2x^{2}+8x+48}{4}\leq \frac{1}{2}(\pi \frac{x^{2}}{4} +\pi \frac{(4-x)^{2}}{4})$
$\Leftrightarrow$ $-2x^{2}+8x+48 \leq \frac{1}{2}(x^{2}+(4-x)^{2}$
$\Leftrightarrow$ $-2x^{2}+8x+48 \leq x^{2}-x+8$
$\Leftrightarrow$ $-2,45 \leq x \leq 5,45$
Mà x > 0 nên ta có: $0 < x \leq 5,45$
Xem toàn bộ: Giải bài 17 Dấu của tam thức bậc hai

Bình luận