Giải bài 4 trang 103 SBT toán 10 tập 1 chân trời

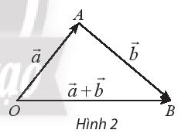
Vẽ ba điểm O, A, B sao cho $\overrightarrow{OA}$ = $\overrightarrow{a}$ , $\overrightarrow{OB}$ = $\overrightarrow{b}$ .

Ta có $\overrightarrow{b}$ = $\overrightarrow{a}$ + $\overrightarrow{b}$ . 

Trong tam giác OAB ta có bất đẳng thức |OA - OB| ≤ OB ≤ OA + AB

=> | $\overrightarrow{a}$ | - | $\overrightarrow{b}$ | ≤ |$\overrightarrow{a}$ + $\overrightarrow{b}$ | ≤ | $\overrightarrow{a}$ | + | $\overrightarrow{b}$ |