Giải bài 2 trang 100 SBT toán 10 tập 1 chân trời
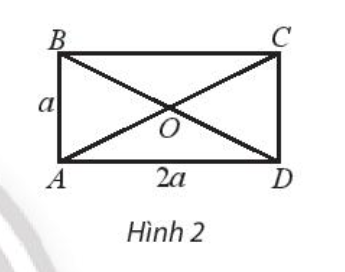
Bài 2 : Cho hình chữ nhật ABCD có tâm O và cho AD = 2a, AB = a. Tính:
a) $\overrightarrow{AB}$ . $\overrightarrow{AO}$ ;
b) $\overrightarrow{AB}$ . $\overrightarrow{AD}$ .
a) cos( $\overrightarrow{OC}$ . $\overrightarrow{OC}$ ) = cosBAC = $\frac{AB}{AC}$ = $\frac{1}{√5}$
Khi đó $\overrightarrow{AB}$ . $\overrightarrow{AO}$ = | $\overrightarrow{AB}$ | . | $\overrightarrow{AO}$ | . cos($\overrightarrow{AB}$ . $\overrightarrow{AO}$)
= a . $\frac{a√5}{2}$ . $\frac{1}{√5}$ = $\frac{a2}{2}$ ;
b) $\overrightarrow{AB}$ . $\overrightarrow{AD}$ = 0.
Từ khóa tìm kiếm Google: Giải bài tập toán 10 sách chân trời, Giải bài tập toán 10, Đáp án bài 4 Tích vô hướng của hai vectơ trang 97 toán 10, Sbt toán 10 bài 4 Tích vô hướng của hai vectơ, Giải toán 10 bài 2 trang 100, Lời giải toán 10 bài 2 trang 100 sách chân trời sáng tạo, toán 10 chân trời sáng tạo trang 100, toán 10 bài 2 trang 100 bài tập

Bình luận