Câu hỏi tự luận mức độ vận dụng Toán 9 ctst bài 3: Định li Viète

Câu 1: 

Ta có 

Vậy a, b là hai nghiệm của phương trình:

Câu 2:

Ta có 

Câu 3: 

a)

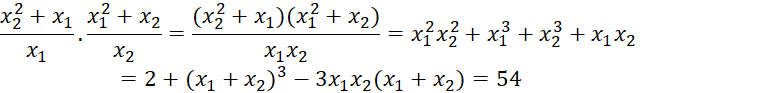
Vậy phương trình bậc hai cần tìm là:

b)

Ta có là nghiệm của phương trình  

Tương tự:

Mà

Vậy phương trình bậc hai cần tìm là:

c)

Đặt 

Vậy phương trình bậc hai cần tìm là:

Câu 4: 

a) Phương trình có nghiệm nên thay vào phương trình ta được:

b) Phương trình có hai nghiệm phân biệt trái dấu khi

c) Phương trình có hai nghiệm phân biệt khi

hoặc .

Theo hệ thức Viète ta có:

Hai nghiệm của phương trình cùng dương khi 

và

Kết hợp với điều kiện ta có hoặc .

Câu 5: 

Đặt , ta có 

Phương trình ẩn là được đưa về phương trình ẩn :

. 

Phương trình ẩn phải có hai nghiệm trái dấu khi

Vậy

Câu 6: 

Phương trình có hai nghiệm phân biệt   

Khi đó: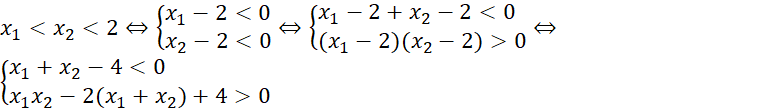

. 

Kết hợp với (*) ta được:

Câu 7: 

Ta có:

Để phương trình có 2 nghiệm phân biệt khi

Theo Viète ta có:

Mà:

(nhận) hoặc (loại)

Vậy thỏa mãn yêu cầu đề bài.

Câu 8: 

Phương trình: (1)

Phương trình (1) là phương trình bậc hai ẩn có: 

>0

Phương trình  có hai nghiệm phân biệt với mọi , mà nên:

thỏa mãn:

hoặc

hoặc

hoặc

Vây tất cả các giá trị của thỏa mãn đề bài là: và .

Câu 9: 

Phương trình có với mọi

Suy ra: phương trình trên luôn có hai nghiệm phân biệt

Theo định lí Viète ta có :

Ta có :

(vì )

Dấu ‘’= ‘’ xảy ra khi và chỉ khi .

Vậy GTNN của C là đạt tại