I. ÔN TẬP KIẾN THỨC CHÍNH CHƯƠNG VIII

Định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

Đường trung bình của tam giác: Đường trung bình của hai tam giác là đoạn nối trung điểm hai cạnh của tam giác đó.

Đường trung bình song song với cạnh thứ ba và bằng nửa cạnh đó.

Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.

Các trường hợp đồng dạng của hai tam giác:

1. Cạnh – cạnh – cạnh

2. Cạnh – góc – cạnh

3. Góc – cạnh – góc 

Các trường hợp đồng dạng của hai tam giác vuông:

1. Cạnh huyền – cạnh góc vuông

2. Hai cạnh góc vuông tỉ lệ với nhau.

3. Hai góc nhọn bằng nhau.

II. LUYỆN TẬP

Đáp án câu hỏi trắc nghiệm 

Câu 3.

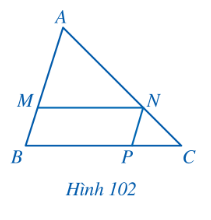
Ta có: NP // AB nên $\frac{NP}{AB}=\frac{CP}{BC}$ (định lí Thalès)

$\frac{MN}{BC}=\frac{BP}{BC}$ (MN = BP do BMNP là hình bình hành)

Suy ra: $\frac{MN}{BC}+\frac{NP}{AB}=\frac{BP}{BC}+\frac{CP}{BC}=\frac{BP+CP}{BC}=\frac{BC}{BC}=1$.

Câu 4.

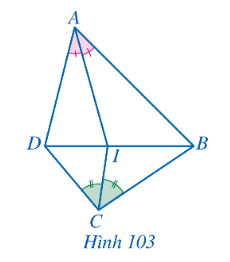
Tam giác ABD có AI là đường phân giác của góc BAD

Suy ra: $\frac{ID}{IB}=\frac{AD}{AB}$ (Tính chất đường phân giác) (1)

Tam giác BCD có CI là đường phân giác của góc BCD

Suy ra: $\frac{ID}{IB}=\frac{CD}{BC}$ (Tính chất đường phân giác) (2)

Từ (1)(2) suy ra: $\frac{AD}{AB}=\frac{CD}{BC}$ hay AB . CD = AD . BC.

Câu 7.

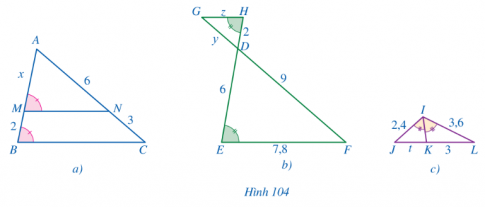
a) Ta có: $\widehat{AMN}=\widehat{ABC}$ và chung góc A

Suy ra: $\triangle$AMN $\sim $ $\triangle$ABC

Do đó: $\frac{AM}{AB}=\frac{AN}{AC}$ hay $\frac{x}{x+2}=\frac{6}{6+3}$

Suy ra: 9x = 6(x + 2)

9x = 6x + 12

3x = 12

x = 4.

Vậy x = 4 (đvđd)

b) Ta có: GH // EF nên $\frac{GH}{EF}=\frac{DG}{DF=\frac{DH}{DE}$ (định lí Thalès)

Hay $\frac{z}{7,8}=\frac{y}{9}=\frac{2}{6}$

Ta có: $\frac{y}{9}=\frac{2}{6}$. Suy ra: y = 3 (đvđd)

$\frac{z}{7,8}=\frac{2}{6}$. Suy ra: z = 2,6 (đvđd)

c) Ta có: IK là đường phân giác của tam giác ILJ

Suy ra: $\frac{JK}{KL}=\frac{IJ}{IL}$ hay $\frac{t}{3}=\frac{2,4}{3,6}$

Do đó: t = 2 (đvđd)

Câu 8.

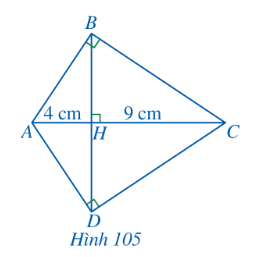
a) Ta có: $\widehat{AHB}=\widehat{ABC}=90^{\circ}$, chung góc A

Suy ra: $\triangle$HAB $\sim $ $\triangle$BAC (1)

Ta có: $\widehat{BHC}=\widehat{ABC}=90^{\circ}$, chung góc C

Suy ra: $\triangle$HBC $\sim $ $\triangle$BAC (2)

Từ (1)(2) suy ra: $\triangle$HAB $\sim $ $\triangle$HBC.

b) $\triangle$HAB $\sim $ $\triangle$HBC (câu a) 

Suy ra: $\frac{HA}{HB}=\frac{HB}{HC}$ hay $\frac{4}{HB}=\frac{HB}{9}$

Do đó: $HB^{2}$ = 36 hay HB = 6 cm (1)

Chứng minh tương tự câu a ta có: $\triangle$HAD $\sim $ $\triangle$HDC

Suy ra: $\frac{HA}{HD}=\frac{HD}{HC}$ hay $\frac{4}{HD}=\frac{HD}{9}$

Do đó: $HD^{2}$ = 36 hay HD = 6 cm (2)

Từ (1), (2) suy ra: HB = HD = 6 cm.

Câu 9.

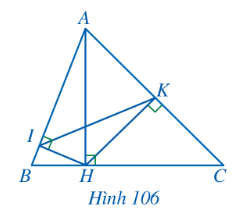
a) Ta có: $\widehat{AIH}=\widehat{AHB}=90^{\circ}$, chung góc A

Suy ra: $\triangle$AIH $\sim $ $\triangle$AHB (g.g)

Do đó: $\frac{AI}{AH}=\frac{AH}{AB}$ hay $AH^{2}$ = AB . AI

Ta có: $\widehat{AKH}=\widehat{AHC}=90^{\circ}$, chung góc A

Suy ra: $\triangle$AKH $\sim $ $\triangle$AHC (g.g)

Do đó: $\frac{AK}{AH}=\frac{AH}{AC}$ hay $AH^{2}$ = AC . AK

Vậy $AH^{2}$ = AB . AI = AC . AK.

b) Ta có: AB . AI = AC . AK (câu a)

Suy ra: $\frac{AB}{AK}=\frac{AC}{AI}$, chung góc A

Do đó: $\triangle$ABC $\sim $ $\triangle$AKI (c.g.c)

Nên $\widehat{AIK}=\widehat{ACB}$ hay $\widehat{AIK}=\widehat{ACH}$.