Lý thuyết trọng tâm toán 8 cánh diều bài 2: Hình chóp tứ giác đều
Tổng hợp kiến thức trọng tâm toán 8 cánh diều bài 2: Hình chóp tứ giác đều. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
I. HÌNH CHÓP TỨ GIÁC ĐỀU
HĐ1:
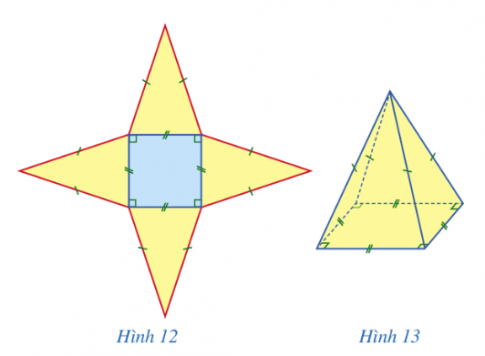
Nhận xét: Hình chóp tứ giác đều có 5 mặt, 8 cạnh.
HĐ2:
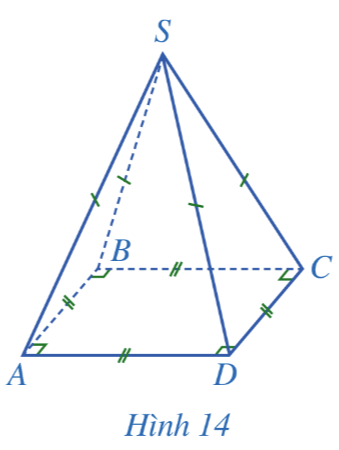
Nhận xét: Ở Hình 14, ta có
- Hình chóp tứ giác đều S.ABCD;
- Mặt đáy ABCD là một hình vuông;
- Các mặt bên SAB, SBC, SCD, SDA là những tam giác cân tại S;
- Các cạnh đáy AB, BC, CD, DA bằng nhau;
- Các cạnh bên SA, SB, SC, SD bằng nhau;
- S gọi là đỉnh của hình chóp tứ giác đều S.ABCD
II. DIỆN TÍCH XUNG QUANH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
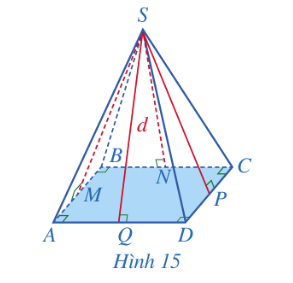
Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.
$S_{xq}=12.C.d$
Trong đó: $S_{xq}$ là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều.
Ví dụ 1 (SGK -tr.85)
Luyện tập
Diện tích xung quanh của hình chóp tứ giác đều đó là:
$S_{xq}=\frac{1}{2}.(10.4).15 $ = 300 ($cm^{2}$)
III. THỂ TÍCH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
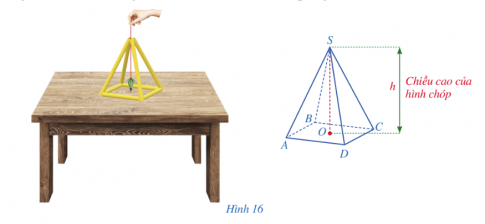
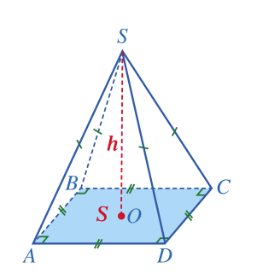
Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.
V = $\frac{1}{3}$. S. h
Trong đó: V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tứ giác đều.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận