CHƯƠNG VII: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

BÀI 22. BA ĐƯỜNG CONIC

1. ELIP

HĐ1.

a) Đường nhận được liên hệ với hình 7.17b.

b) Tổng các khoảng cách từ đầu bút tới các vị trí F$_{1}$, F$_{2}$ không thay đổi vì nó luôn bằng độ dài dây.

Định nghĩa:

Cho hai điểm cố định và phân biệt F$_{1}$, F$_{2}$. Đặt F$_{1}$F$_{2}$=2c>0. Cho số thực a lớn hơn c. Tập hợp các điểm M sao cho MF$_{1}$+MF$_{2}$=2a được gọi là đường elip (hay elip). Hai điểm F$_{1}$, F$_{2}$ được gọi là hai tiêu điểm và F$_{1}$F$_{2}$=2c được gọi là tiêu cự của elip đó.

Thách thức nhỏ: Xét tam giác MF$_{1}$F$_{2}$ có: MF$_{1}$+MF$_{2}$=2a>F$_{1}$F$_{2}$=2c (bất đẳng thức tam giác). Suy ra: a>c.

Ví dụ 1 (SGK – tr.49)

Luyện tập 1

Ta có vị trí ban đầu của bi và vị trí của lỗ thu là 2 tiêu điểm của hình elip, gọi lần lượt là F$_{1}$ và F$_{2}$. Bi lăn từ F$_{1}$ đến một vị trí M trên hình elip rồi đi đến F$_{2}$. Vậy quãng đường bi đi được là: MF$_{1}$+MF$_{2}$

Theo tính chất hình elip thì MF$_{1}$+MF$_{2}$=2a, không đổi

Suy ra độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu không phụ thuộc vào đường đi của bi.

HĐ2. 

a) Vì F$_{1}$F$_{2}$=2c, mà O là trung điểm của F$_{1}$,F$_{2}$

Tọa độ của các điểm: F$_{1}$(-c;0) và F$_{2}$(c;0)

b) Giả sử M thuộc elip (E) ta chứng minh:

$\sqrt{(x+c)^{2}+y^{2}}$+$\sqrt{(x-c)^{2}+y^{2}}$=2a   (1) 

Thật vậy: M thuộc elip (E) nên: MF$_{1}$+MF$_{2}$=2a hay $\sqrt{(x+c)^{2}+y^{2}}$+$\sqrt{(x-c)^{2}+y^{2}}$=2a

Giả sử $\sqrt{(x+c)^{2}+y^{2}}$+$\sqrt{(x-c)^{2}+y^{2}}$=2a ta chứng minh M thuộc elip (E). Thật vậy:

$\sqrt{(x+c)^{2}+y^{2}}$+$\sqrt{(x-c)^{2}+y^{2}}$=2a nên MF$_{1}$+MF$_{2}$=2a

⇒ M thuộc elip (E).

Chú ý: Người ta có thể biến đổi (1) về dạng $\frac{x^{2}}{a^{2}}$+$\frac{y^{2}}{b^{2}}$=1, với b=$\sqrt{a^{2}-c^{2}}$

Kết luận: 

Trong mặt phẳng toạ độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình

$\frac{x^{2}}{a^{2}}$+$\frac{y^{2}}{b^{2}}$=1, với a>b>0   (2)

Ngược lại, mỗi phương trình có dạng (2)  đều là phương trình của elip có hai tiêu điểm F$_{1}$(-$\sqrt{a^{2}-b^{2}}$;0), F$_{2}$(a$\sqrt{a^{2}-b^{2}}$;0), tiêu cự 2c=2$\sqrt{a^{2}-b^{2}}$ và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a.

Phương trình (2) được gọi là phương trình chính tắc của elip tương ứng.

Ví dụ 2 (SGK – tr.50)

Luyện tập 2

Có: a$^{2}$=100, b$^{2}$=64⇒c=$\sqrt{a^{2}+b^{2}}$=6. Vậy elip có hai tiêu điểm là F$_{1}$(-6; 0) và F$_{2}$(6; 0)  và tiệu cự là F$_{1}$F$_{2}$=2c=12.

Vận dụng 1

Ta có 75cm trên thực tế ứng với 2,5 đơn vị trên mặt phẳng tọa độ.

Gọi điểm M trên elip thỏa mãn có hoành độ là 2,5 tọa độ M(2,5; y)

Mà M thuộc (E) nên: $\frac{2,5^{2}}{16}$+$\frac{y^{2}}{4^{2}}$=1

y$^{2}$=$\frac{39}{16}$nên y≈1,56

Vậy chiều cao của ô thoáng là: 

h = 1,56.30=46,8 cm.

2. HYPEBOL

HĐ3.

a) Giả sử nơi phát ra tín hiệu âm thanh là tại vị trí điểm M. 

Khi đó MF$_{1}$ là khoảng cách từ nơi phát ra tín hiệu âm thanh tới F$_{1}$ và MF$_{2}$ là khoảng cách từ nơi phát ra tín hiệu âm thanh tới F$_{2}$.

Gọi t$_{1}$ là thời gian âm thanh phát từ M đến F$_{1}$, t$_{2}$ là thời gian âm thanh phát từ M đến F$_{2}$. 

Thiết bị tại F$_{2}$ nhận được tín hiệu âm thanh sớm hơn thiết bị tại F$_{1}$ là 2 giây nên t$_{1}$ – t$_{2}$ = 2. 

Vận tốc âm thanh là 343 m/s. 

Khi đó ta có: MF$_{1}$ = 343t$_{1}$; MF$_{2}$ = 343t$_{2}$. 

Suy ra: MF$_{1}$ – MF$_{2}$ = 343.t$_{1}$ – 343.t$_{2}$ = 343(t$_{1}$ – t$_{2}$) = 343. 2 = 686 (m). 

Vậy mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F$_{1}$, F$_{2}$ là MF$_{1}$ – MF$_{2}$ = 686 (m). 

b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh chính là việc giải quyết bài toán tìm tập hợp những điểm M thỏa mãn MF$_{1}$ – MF$_{2}$ = 686 (m). 

Định nghĩa:

Cho hai điểm cố định và phân biệt F$_{1}$, F$_{2}$. Đặt F$_{1}$F$_{2}$=2c. Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho |MF$_{1}$-MF$_{2}$|=2a được gọi là đường hypebol (hay hypebol). Hai điểm F$_{1}$, F$_{2}$ được gọi là hai tiêu điểm và F$_{1}$F$_{2}$=2c được gọi là tiêu cự của hypebol đó.

Thách thức nhỏ: Xét tam giác MF$_{1}$F$_{2}$ có: |MF$_{1}$-MF$_{2}$|=2a<F$_{1}$F$_{2}$=2c (bất đẳng thức tam giác). Suy ra: a<c.

Chú ý: Hypebol có hai nhánh (H.7.23), một nhánh gồm những điểm M thoả mãn MF$_{1}$-MF$_{2}$=2a và nhánh còn lại gồm những điểm M thoả mãn MF$_{1}$-MF$_{2}$=-2a (hay MF$_{2}$-MF$_{1}$=2a)

Ví dụ 3 (SGK – tr.51)

Luyện tập 3

Do M, N tương ứng là trung điểm của các cạnh AB, CD và tính chất hình chữ nhật ABCD ta có: BM=CN=AM=DN.

Vì BM=DN, BM//DN

⇒BMDN là hình bình hành

⇒BN=DM.

Tương tự CM=AN

Ta chứng minh được BMNC là hình chữ nhật ⇒BN=CM

⇒BN=DM=CM=AN.

Từ đó: |BN-BM|=|CN-CM|= |AN-AM|=|DN-DM|>MN (bất đẳng thức tam giác).

Vậy A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

HĐ4.

a) Vì F$_{1}$F$_{2}$=2c, mà O là trung điểm của F$_{1}$,F$_{2}$

Tọa độ của các điểm: F$_{1}$(-c;0) và F$_{2}$(c;0)

b) Giả sử M thuộc hypebol (H) ta chứng minh: 

|$\sqrt{(x+c)^{2}+y^{2}}$-$\sqrt{(x-c)^{2}+y^{2}}$|=2a   (3) 

Thật vậy: M thuộc elip (E) nên: |MF$_{1}$-MF$_{2}$|=2a

Giả sử |$\sqrt{(x+c)^{2}+y^{2}}$-$\sqrt{(x-c)^{2}+y^{2}}$|=2a ta chứng minh M thuộc hypebol (H). Thật vậy:

|$\sqrt{(x+c)^{2}+y^{2}}$-$\sqrt{(x-c)^{2}+y^{2}}$|=2a nên |MF$_{1}$-MF$_{2}$|=2a

⇒ M thuộc hypebol (H).

Chú ý: Người ta có thể biến đổi (3) về dạng $\frac{x^{2}}{a^{2}}$-$\frac{y^{2}}{b^{2}}$=1, với b=$\sqrt{c^{2}-a^{2}}$

Kết luận: 

Trong mặt phẳng toạ độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình

$\frac{x^{2}}{a^{2}}$-$\frac{y^{2}}{b^{2}}$=1, với a,b>0   (4)

Ngược lại, mỗi phương trình có dạng (4)  đều là phương trình của hypebol có hai tiêu điểm F$_{1}$(-$\sqrt{a^{2}+b^{2}}$;0), F$_{2}$($\sqrt{a^{2}+b^{2}}$;0), tiêu cự 2c=2$\sqrt{a^{2}+b^{2}}$ và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đó tới hai tiêu điểm bằng 2a.

Phương trình (2) được gọi là phương trình chính tắc của hypebol tương ứng.

Ví dụ 4 (SGK – tr.52)

Luyện tập 4

Có: a$^{2}$=144, b$^{2}$=25⇒c=$\sqrt{a^{2}+b^{2}}$=13. Vậy elip có hai tiêu điểm là F$_{1}$(-13; 0) và F$_{2}$(13; 0)  và tiệu cự là F$_{1}$F$_{2}$=2c=26.

3. PARABOL

HĐ5.

Ta có: MF=$\sqrt{x^{2}+(y-1)^{2}}$,

d(M;∆)=$\frac{\left | y+1 \right |}{\sqrt{1^{2}+0}}$=|y+1|

+ Giả sử MF=d(M;∆), ta chứng minh M(x;y) thuộc (P). Thật vậy 

MF=d(M;∆) <=> $\sqrt{x^{2}+(y-1)^{2}}$=|y+1|

x$^{2}$+(y-1)$^{2}$=(y+1)$^{2}$

x$^{2}$-4y=0⇔y=$\frac{1}{4}$x$^{2}$

Vậy M thuộc (P)

+ Giả sử M(x;y) thuộc (P), ta chứng minh MF=d(M;∆)

M thuộc P⇒y=$\frac{1}{4}$x$^{2}$ hay x$^{2}$=4y thay vào biểu thức MF có: 

MF=$\sqrt{x^{2}+(y-1)^{2}}$

=$\sqrt{4y+(y-1)^{2}}$

=$\sqrt{y^{2}+2y+1}$

=$\sqrt{(y+1)^{2}}$

=|y+1|=d(M;∆)

Vậy MF=d(M;∆)

Định nghĩa:

Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F. Tập hợp các điểm M cách đều F và ∆ được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, ∆ được gọi là đường chuẩn, khoảng cách từ F đến ∆ được gọi là tham số tiêu của parabol đó.

HĐ6.

a) Do O là trung điểm HF, mà HF = p (tham số tiêu của (P)) nên tọa độ của F là: F($\frac{p}{2}$;0).

Đường thẳng Δ đi qua H(-$\frac{p}{2}$;0) và vuông góc với trục Ox nên có phương trình: x=-$\frac{p}{2}$

b) Ta có: MF=$\sqrt{(x-\frac{p}{2})^{2}+y^{2}}$

d(M,∆)=$\frac{\left | x+\frac{-p}{a} \right |}{\sqrt{1^{2}+0}}$=|x+$\frac{-p}{a}$|

+ Giả sử M thuộc (P), ta chứng minh

$\sqrt{(x-\frac{p}{2})^{2}+y^{2}}$=|x+$\frac{-p}{a}$|

Thật vậy: M thuộc P⇒MF=d(M,∆)

<=> $\sqrt{(x-\frac{p}{2})^{2}+y^{2}}$=|x+$\frac{-p}{a}$|

+ Giả sử 

$\sqrt{(x-\frac{p}{2})^{2}+y^{2}}$=|x+$\frac{-p}{a}$|

Ta chứng minh M thuộc (P). Thật vậy:

$\sqrt{(x-\frac{p}{2})^{2}+y^{2}}$=|x+$\frac{-p}{a}$|⇒MF=d(M,∆)

Vậy M thuộc (P).

Chú ý: Bình phương hai vế của phương trình trên rồi rút gọn, ta dễ dạng nhận được phương trình y$^{2}$=2px.

Định nghĩa: 

Xét (P) là một parabol với tiêu điểm F, đường chuẩn ∆. Gọi H là hình chiếu vuông góc của F trên ∆. Khi đó, trong hệ trục toạ độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình 

y$^{2}$=2px  (với p>0)      (5)

Phương trình (5) được gọi là phương trình chính tắc của parabol (P).

Ngược lại, mỗi phương trình dạng (5), với p>0, là phương trình chính tắc của parabol có tiêu điểm F($\frac{p}{2}$;0) và đường chuẩn ∆:x=-$\frac{p}{2}$.

Ví dụ 5 (SGK – tr.53)

Vận dụng 2

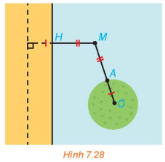
Trong mô hình này, ta có:

MO=MA+R=MH+R (R là bán kính đảo).

Gọi d là đường bờ biển. Gọi ∆ là đường thẳng nằm tròn đất liền, song sng với d, cách d một khoảng R=OA. Ta có:

d(M; ∆) =MH+R=MA+AO=MO

Vậy tập hợp các điểm M thuộc đường parabol (P) có tiêu điểm là O, đường chuẩn là ∆. Vậy đường ranh giới cần tìm là đường parabol (P)

4. MỘT SỐ ỨNG DỤNG CỦA BA ĐƯỜNG CONIC

a) Tính chất quang học

Tương tự gương cầu lồi thường đặt ở những khúc cua, người ta cũng có những gương (lồi, lõm) elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phản xạ theo một quy tắc được xác định rõ bằng hình học. Chẳng hạn:

- Tia sáng phát ra từ một tiêu điểm của elip, parabol (đối với các gương lõm elip, hypebol) sau khi gặp elip, hypebol sẽ bị hắt lại theo một tia (tia phản xạ) nằm trên đường thẳng đi qua tiêu điểm còn lại. (H.7.29)

- Tia sáng hướng tới một tiêu điểm của elip, hypebol (đối với các gương elip, hypebol lồi), khi gặp elip, hypebol sẽ bị hắt lại theo một tia nằm trên đường thẳng đi qua tiêu điểm còn lại (H.7.30).

- Với gương parabol lõm, tia sáng phát ra từ tiêu điểm khi gặp parabol sẽ bị hắt lại theo một tia vuông góc với đường chuẩn của parabol (H.7.31). Ngược lại, nếu tia tới vuông góc với đường chuẩn của parabol thì tia phản xạ sẽ đi qua tiêu điểm của parabol

=> Tính chất quang học được đề cập ở trên giúp ta nhận được ánh sáng mạnh hơn khi các tia sáng hội tu và giúp ta đổi hướng ánh sáng khi cần. Ta cũng có điều tương tự đối với tín hiệu âm thanh, tín hiệu truyền từ vệ tinh.

b) Một số ứng dụng

- Ba đường conic xuất hiện trong khoa học và trong cuộc sống, chẳng hạn:

+ Tia nước bắn ra từ đài phun nước, đường đi bổng của quả bóng

+ Khi nghiêng cốc nước hình trụ, mặt nước có hình elip

+ Ánh sáng phát ra từ một bóng đèn Led trên trần nhà

+ Nhiều công trình kiến trúc có hình elip, parabol hay hypebol

- Ba đường conic có nhiều ứng dụng trong khoa học và trong cuộc sống, chẳng hạn:

+ Trong vũ trụ bao la, ánh sáng đóng vai trò sứ giả truyền tin

+ Trong thiên văn học, các gương trong kính thiên văn giúp các nhà khoa học nhận được hình ảnh quan sát rõ nét hơn, ánh sáng thu được có các chỉ số phân tích rõ hơn

+ Ăng-ten vệ tinh parabol là thiết bị thu tín hiệu truyền về từ vệ tinh

+ Đèn pha đáy parabol giúp ánh sáng có thể phát xa

+ Trong y học, tia laser dùng để tán sỏi thận

+ Tháp giải nhiệt hình hypebol giúp quá trình toả nhiệt được thuận lợi.

Vận dụng 3: 

Khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán là tiêu cự.

Ta có: a$^{2}$=400, b$^{2}$=76, c=$\sqrt{(a^{2}-b^{2}}$=18 nên tiêu cự là 2c = 36.

Vậy khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán là 36 cm.