CHƯƠNG VII: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

BÀI 19. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG

HĐ1.

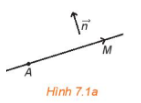
Tập hợp những điểm M là đường thẳng qua A và vuông góc với với giá của $\underset{n}{\rightarrow}$.

Định nghĩa: Vectơ $\underset{n}{\rightarrow}$ khác $\underset{0}{\rightarrow}$ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu giá của nó vuông góc với ∆.

Nhận xét:

- Nếu $\underset{n}{\rightarrow}$ là vectơ pháp tuyến của đường thẳng ∆ thì k$\underset{n}{\rightarrow}$ (k≠0) cũng là vectơ pháp tuyến của ∆.

- Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ pháp tuyến của nó.

Ví dụ 1 (SGK – tr.31)

HĐ2.

$\underset{AM}{\rightarrow}$=(x-x$_{0}$;y-y$_{0}$)

Xét tích $\underset{n}{\rightarrow}$. $\underset{AM}{\rightarrow}$=a(x-x$_{0}$)+b(y-y$_{0}$)=0  (1)

$\underset{n}{\rightarrow} \perp \underset{AM}{\rightarrow}$ hay $\underset{AM}{\rightarrow}$ có giá trùng với đường thẳng ∆ ⇒M∈∆

Nhận xét:

Nếu đặt c=-ax$_{0}$-by$_{0}$ thì (1) còn được viết dưới dạng ax+by+c=0 và được gọi là phương trình tổng quát của ∆ khi và chỉ khi toạ độ của nó thoả mãn phương trình tổng quát của ∆.

Kết luận:

Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax+by+c=0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax+by+c=0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận $\underset{n}{\rightarrow}$(a;b) là một vectơ pháp tuyến.

Ví dụ 2 (SGK – tr.31)

Luyện tập 1:

Đường cao AH đi qua điểm A(-1;5) có một vectơ pháp tuyến là

$\underset{n_{AH}}{\rightarrow}$=$\underset{BC}{\rightarrow}$=(4;-2).

Phương trình tổng quát của AH là: 4(x+1)-2(y-5)=0

⇔4x-2y+14=0

Ví dụ 2 (SGK – tr.32)

Luyện tập 2:

Ta có: ∆:y=3x+4

⇔∆:3x-y+4=0

Một vectơ pháp tuyến của đường thẳng ∆ là $\underset{n}{\rightarrow}$=(3;-1)

Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng ∆:ax+by+c=0

+) Nếu b=0 thì phương trình có thể đưa về dạng x=m (với m=-$\frac{c}{a}$) và ∆ vuông góc với Ox

+) Nếu b≠0 thì phương trình có thể đưa về dạng y=nx+p (với n=-$\frac{a}{b}$,  p=-$\frac{c}{b}$)

2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

HĐ3.

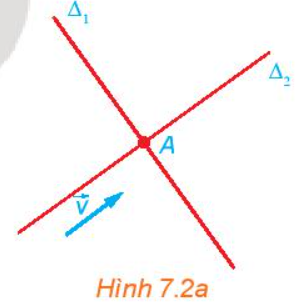
Vật thể chuyển động với vectơ vận tốc bằng $\underset{v}{\rightarrow}$ thì nó sẽ di chuyển trên đường thẳng ∆$_{2}$.

Định nghĩa: Vectơ $\underset{u}{\rightarrow}$ khác $\underset{0}{\rightarrow}$ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu giá của nó song song hoặc trùng với ∆.

Nhận xét:

- Nếu $\underset{u}{\rightarrow}$ là vectơ chỉ phương của đường thẳng ∆ thì k$\underset{u}{\rightarrow}$ (k≠0) cũng là vectơ chỉ phương của ∆.

- Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ chỉ phương của nó.

- Vectơ $\underset{n}{\rightarrow}$(a;b) vuông góc với các vectơ $\underset{u}{\rightarrow}$(-b;a) và $\underset{v}{\rightarrow}$(b;-a) nên nếu $\underset{n}{\rightarrow}$ là vectơ pháp tuyến của đường thẳng ∆ thì $\underset{u}{\rightarrow}$,$\underset{u}{\rightarrow}$ là hai vectơ chỉ phương của đường thẳng đó và ngược lại.

Ví dụ 4 (SGK – tr.33)

Luyện tập 3:

Ta có: ∆:2x-y+1=0

Một vectơ pháp tuyến của đường thẳng ∆ là $\underset{n}{\rightarrow}$=(2;-1)⇒ vectơ chỉ phương của đường thẳng ∆ là $\underset{u}{\rightarrow}$=(1;2)

HĐ4.

a) Vật thể chuyển động trên đường thẳng qua A(2;1) và có vectơ chỉ phương $\underset{v}{\rightarrow}$(3;4).

b) Giả sử tại thời điểm t, vật thể ở vị trí M(x;y). Khi đó $\underset{AM}{\rightarrow}$=t$\underset{v}{\rightarrow}$ tức là:

$\left\{\begin{matrix}x-2=3t & \\ y-1=4t & \end{matrix}\right.$

<=> $\left\{\begin{matrix}x=2+3t & \\ y=1+4t & \end{matrix}\right.$

Vậy M(2+3t;1+4t)

Định nghĩa: Cho đường thẳng ∆ đi qua điểm A(x$_{0}$;y$_{0}$)và có vectơ chỉ phương $\underset{u}{\rightarrow}$(a;b). Khi đó điểm M(x;y) thuộc đường thẳng ∆ khi và chỉ khi tồn tại số thực t sao cho $\underset{AM}{\rightarrow}$=t$\underset{u}{\rightarrow}$, hay $\left\{\begin{matrix}x=x_{0}+at & \\ y=y_{0}+bt & \end{matrix}\right.$     (2)

Hệ (2) được gọi là phương trình tham số của đường thẳng ∆ (t là tham số).

Ví dụ 5 (SGK – tr.33)

Luyện tập 4:

Ta có: d:3x-4y-1=0

$\underset{n_{d}}{\rightarrow}$=(2;-1)⇒$\underset{n_{d}}{\rightarrow}$=(1;2)

Vì ∆//d⇒$\underset{u_{\Delta }}{\rightarrow}$=$\underset{u_{d}}{\rightarrow}$=(1;2)

Phương trình tham số của đường thẳng ∆ đi qua M(2;-3) và có vectơ chỉ phương $\underset{u_{\Delta }}{\rightarrow}$=(1;2) là: 

$\left\{\begin{matrix}x=-1+4t & \\ y=2+3t & \end{matrix}\right.$ .

Ví dụ 6 (SGK – tr.33)

Luyện tập 5:

Ta có: A(x$_{1}$;y$_{1}$), B(x$_{2}$;y$_{2}$)

$\underset{u_{AB}}{\rightarrow}$=$\underset{AB}{\rightarrow}$=(x$_{2}$-x$_{1}$; y$_{2}$-y$_{1}$)

Phương trình tham số của đường thẳng AB:

$\left\{\begin{matrix}x=x_{1}+(x_{2}-x_{1})t & \\ y=y_{1}+(y_{2}-y_{1})t & \end{matrix}\right.$ 

Vì $\underset{u_{AB}}{\rightarrow}$=(x$_{2}$-x$_{1}$; y$_{2}$-y$_{1}$)

$\underset{n_{AB}}{\rightarrow}$=(y$_{2}$-y$_{1}$; -x$_{2}$+x$_{1}$)

Phương trình tổng quát của đường thẳng AB: 

(y$_{2}$-y$_{1}$)(x-x$_{1}$) -(x$_{2}$-x$_{1}$)(y-y$_{1}$)=0

Vận dụng:

Ta có: A(0;32), B(100;212)

Vì $\underset{u_{AB}}{\rightarrow}$=Vì $\underset{AB}{\rightarrow}$=(100; 180)

Vì $\underset{n_{AB}}{\rightarrow}$=(9;-5)

Phương trình đường thẳng AB đi qua A(0;32) và có Vì $\underset{n_{AB}}{\rightarrow}$=(9;-5) là:

9x-5y+160=0

⇔x=$\frac{5y-160}{9}$

Khi y=0℉ ta có:

x=$\frac{5.0-160}{9}$=(-$\frac{160}{9}$)℃

Khi y=100℉ ta có:

x=$\frac{5.100-160}{9}$=($\frac{340}{9}$)℃

Vậy 0℉, 100℉ tương ứng xấp xỉ -18℃, 38℃