I. KHÁI NIỆM ĐIỆN TRƯỜNG

Bài 1: Đặt điện tích q cách điện tích Q một khoảng r (Hình 17.1)...

Đáp án:

1. Không phải. Điện trường xung quanh điện tích đã truyền tương tác điện và khi đặt trong chân không vẫn xảy ra tương tác này.

2. Ta có thể đặt một điện tích điểm vào trong đó, nếu có lực tác dụng lên điện tích thì tồn tại điện trường, nếu không có lực tác dụng lên điện tích thì không tồn tại điện trường.

II. CƯỜNG ĐỘ ĐIỆN TRƯỜNG

Bài 1: Hãy chứng tỏ rằng vectơ cường độ điện trường...

Đáp án:

Dựa vào công thức: $\underset{E}{\rightarrow}$=$\frac{\underset{F}{\rightarrow}}{q}$

• $\underset{E}{\rightarrow}$ có phương trùng với phương của $\underset{F}{\rightarrow}$

• Với q > 0 thì $\underset{E}{\rightarrow}$, $\underset{F}{\rightarrow}$ cùng chiều với nhau

• Với q < 0 thì $\underset{E}{\rightarrow}$ , $\underset{F}{\rightarrow}$ ngược chiều với nhau

• Nếu q = 1 thì E = F

Bài 2: Xét điện trường của điện tích...

Đáp án:

Cường độ điện trường tại một điểm cách Q một khoảng 3cm: 

$E_{3cm}$=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}r^{2}}$=$\frac{6.10^{-14}}{4\pi .\varepsilon _{0}.0.03^{2}}$=0,6=1.$\frac{10^{-10}}{6\pi \varepsilon _{0}}$ (V/m)

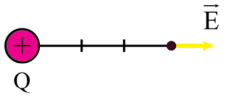
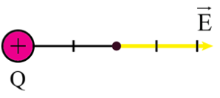
Cường độ điện trường tại một điểm cách Q 2cm:

 $E_{2cm}$=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}r^{2}}$=1,35=2,25.$\frac{10^{-10}}{6\pi \varepsilon _{0}}$ (V/m)(V/m)

Bài 3: Hãy chứng tỏ rằng: Độ lớn cường độ điện trường tại...

Đáp án:

Dựa vào công thức: E=$\frac{F}{Q}$ với Q = 1 C thì E = F

Bài 4: Một điện tích điểm Q = 6.10$^{-13}$ C đặt trong chân không...

Đáp án:

a) Vecto cường độ điện trường có phương trùng với đường thẳng nối điện tích và điểm cần tính,  Q > 0 => chiều hướng ra xa điện tích

$E_{1cm}$=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}.0,01^{2}}$=54 (V/m)

$E_{2cm}$=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}.0,02^{2}}$=13,5 (V/m)

$E_{3cm}$=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}.0,03^{2}}$=6 (V/m)

b) Càng gần điện tích thì điện trường càng mạnh, cường độ điện trường càng lớn. Càng xa điện tích thì điện trường càng yếu, cường độ điện trường càng nhỏ.

c)  Cường độ điện trường tại điểm M cách điện tích Q một khoảng r

- Phương QM

- Chiều từ Q đến M

- Độ lớn: E=$\frac{\left | Q \right |}{4\pi \varepsilon _{0}r^{2}}$. 

Những điểm có cùng khoảng cách đến Q cường độ điện trường sẽ có độ lớn bằng nhau, những điểm ở gần Q hơn sẽ có độ lớn cường độ điện trường lớn hơn và ngược lại.

Bài 4: Nếu trong không gian có hai điện tích điểm dương...

Đáp án:

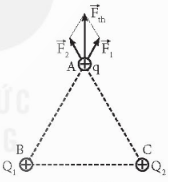
Sử dụng quy tắc hình bình hành $\underset{F_{1}}{\rightarrow}$+$\underset{F_{2}}{\rightarrow}$=$\underset{F}{\rightarrow}$

Bài 5: Đặt điện tích điểm...

Đáp án:

Cường độ điện trường bằng 0 khi:

$\underset{E_{1}}{\rightarrow}$+$\underset{E_{2}}{\rightarrow}$=$\underset{E}{\rightarrow}$=0 ⇒ $\underset{E_{1}}{\rightarrow}$=-$\underset{E_{2}}{\rightarrow}$

=> $\underset{E_{1}}{\rightarrow}$ và $\underset{E_{2}}{\rightarrow}$ ngược chiều và $E_{1}$ = $E_{2}$

$\underset{E_{1}}{\rightarrow}$ và $\underset{E_{2}}{\rightarrow}$ ngược chiều, 2 điện tích trái dấu, |$q_{1}$|>|$q_{2}$|  => điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần B hơn (vì khoảng cách tỷ lệ thuận với độ lớn điện tích)

$\Rightarrow\left\{\begin{matrix}r_{1}-r_{2}=AB\\ \frac{r_{1}^{2}}{r_{2}^{2}}=\frac{\left|q_{1}\right|}{\left|q_{2}\right|}\end{matrix}\right.$ 

⇒ $r_{1}$=0,071m; $r_{2}$=0,041m

Vậy điểm cần tìm cách A 7,1 cm và cách B 4,1 cm

Bài 6: Cho tam giác ABC vuông tại A có AB = 3 cm...

Đáp án:

a) Tại A ta có:

$E_{1}$=$\frac{\left | Q_{1} \right |}{4\pi \varepsilon _{0}AB^{2}}$=$\frac{5.10^{-6}}{8\pi \varepsilon _{0}}$ (V/m) 

$E_{2}$=$\frac{\left | Q_{2} \right |}{4\pi \varepsilon _{0}AC^{2}}$=$\frac{25.10^{-5}}{4\pi \varepsilon _{0}}$ (V/m) 

b) Tại A, 2 vecto cường độ điện trường vuông góc với nhau 

$E_{A}$=$\sqrt{E_{1}^{2}+E_{2}^{2}}$=463427 (V/m)

Bài 7: Một hạt bụi mịn loại...

Đáp án:

Ta có: Lực điện tác dụng vào hạt bụi trong điện trường là: 

F = EQ = 120.1,6.10$^{−19}$ = 1,92.10$^{−17}$

Hạt bụi mịn chịu tác dụng của từ trường Trái Đất phương thẳng đứng xuống dưới, lực điện cùng chiều điện trường do hạt mang điện tích dương khiến hạt thường lơ lửng trong không khí.

III. ĐIỆN PHỔ

Bài 1: Em hãy quan sát Hình 17.6 và đưa ra nhận xét về đặc điểm của...

Đáp án:

a) Đường sức điện dày.
b) Đường sức điện thưa.
c) Các đường  sức điện đi ra từ điện tích âm và kết thúc ở điện tích âm, hoặc từ một điện tích ra vô cùng.

d) Các đường sức là 1 đường cong khép kín

Bài 2: Quan sát Hình 17.7 và các...

Đáp án: