Bài 2.11 trang 44 chuyên đề toán 12

Một cửa hàng chuyên về cà phê, có sẵn 75 kg cà phê Colombia nguyên chất và 120 kg cà phê thương hiệu của cửa hàng. Những thứ này sẽ được pha thành các gói cà phê 1 kg như sau: Một gói tiêu chuẩn có chứa 250 g cà phê Colombia nguyên chất và 750 g cà phê thương hiệu; một gói cao cấp chứa 500 g cà phê Colombia nguyên chất và 500 g cà phê thương hiệu.

a) Gọi x là số gói cà phê tiêu chuẩn và y là số gói cà phê cao cấp, hãy viết hệ bất phương trình bậc nhất mô tả số lượng gói có thể của mỗi loại.

b) Biểu diễn hình học miền nghiệm của hệ bất phương trình bậc nhất nhận được ở câu a và tìm các đỉnh miền nghiệm.

c) Lợi nhuận của mỗi gói cà phê tiêu chuẩn là 30 nghìn đồng và mỗi gói cà phê cao cấp là 40 nghìn đồng. Hỏi cần chuẩn bị bao nhiêu gói cà phê mỗi loại để lợi nhuận thu được là lớn nhất? Giả sử rằng tất cả các gói cà phê đã chuẩn bị đều có thể bán được.

Giải nhanh:

a)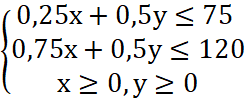

b) 

A(0; 150), B(90; 105); C(160,0)

c) Lợi nhuận thu được là: F(x; y) 30x + 40y max

Ta có:

F(0; 150)  = 6000.

F(90; 105) = 6900.

F(160; 0) = 4800.

Vậy để lợi nhuận lớn nhất cần chuẩn bị 90 gói cà phê tiêu chuẩn và 105 gói cà phê cao cấp.

Bài 2.12 trang 44 chuyên đề toán 12

Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể sử dụng nhiều nhất là 70 giờ, máy thứ hai nhiều nhất là 40 giờ và máy thứ ba nhiều nhất là 90 giờ. Sản phẩm thứ nhất cần 2 giờ trên máy I, 1 giờ trên máy II và 1 giờ trên máy III; sản phẩm thứ hai cần 1 giờ trên máy I, II và 3 giờ trên máy III. Nếu lợi nhuận là 400 nghìn đồng/đơn vị cho sản phẩm thứ nhất và 600 nghìn đồng/đơn vị cho sản phẩm thứ hai, thì cẩn sản xuất bao nhiêu đơn vị mỗi sản phẩm để lợi nhuận thu được là lớn nhất?

Giải nhanh:

Gọi số đơn vị mỗi sản phẩm của hai loại lần lượt là x và y.

F(x; y) = 400x + 600y max

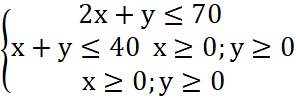
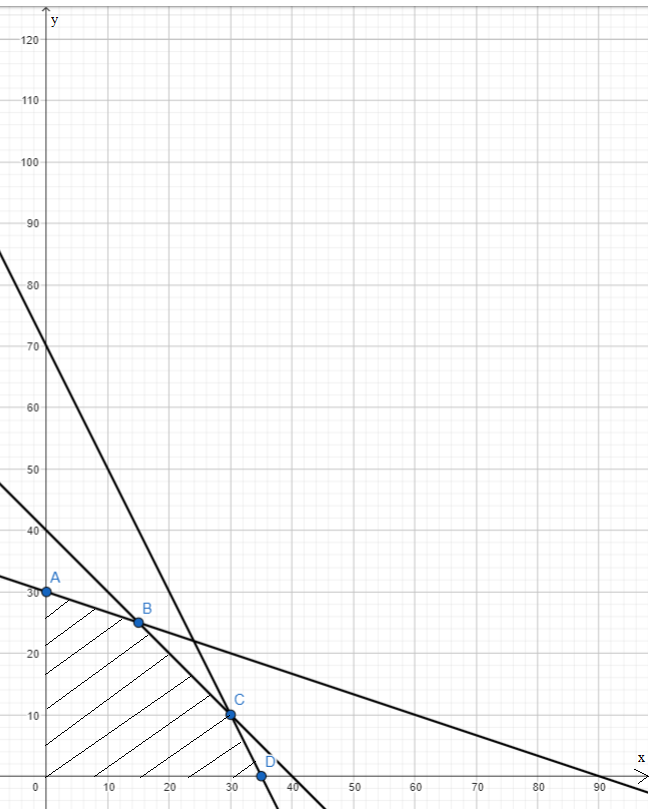
A(0; 30), B(15; 25), C(30; 10), D(35; 0)

Ta có: 

F(0; 30) = 18000.

F(15; 25) = 21000.

F(30; 10) = 18000.

F(35; 0) = 14000.

Vậy để lợi nhuận cao nhất thì cần 15 sản phẩm thứ nhất và 25 sản phẩm thứ hai.

Bài 2.13 trang 44 chuyên đề toán 12

Một công ty bán hàng toàn quốc đang lên kế hoạch tổ chức cuộc họp bán hàng tại Đà Nẵng. Giá vé máy bay khứ hồi thấp nhất từ Hà Nội đến Đà Nẵng là 2 triệu đồng và giá vé khứ hồi thấp nhất từ Thành phố Hồ Chí Minh đến Đà Nẵng là 2,4 triệu đồng. Có 28 đại diện bán hàng ở Hà Nội và 22 đại diện bán hàng ở Thành phố Hồ Chí Minh có thể đến Đà Nẵng dự cuộc họp này. Tổng cộng ít nhất 40 đại diện bán hàng ở Hà Nội và Thành phố Hồ Chí Minh phải tham dự cuộc họp này với ít nhất 12 người từ Hà Nội và 16 người từ Thành phố Hồ Chí Minh. Cần cử bao nhiêu đại diện ở Hà Nội và bao nhiêu đại diện ở Thành phố Hồ Chí Minh đến dự cuộc họp bán hàng ở Đà Nẵng để tổng chi phí vé máy bay là nhỏ nhất?

Giải nhanh:

Gọi số đại diện ở Hà Nội và Thành phố Hồ Chí Minh tham dự lần lượt là x và y.

F(x; y) = 2x + 2,4y min

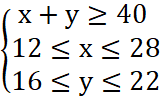
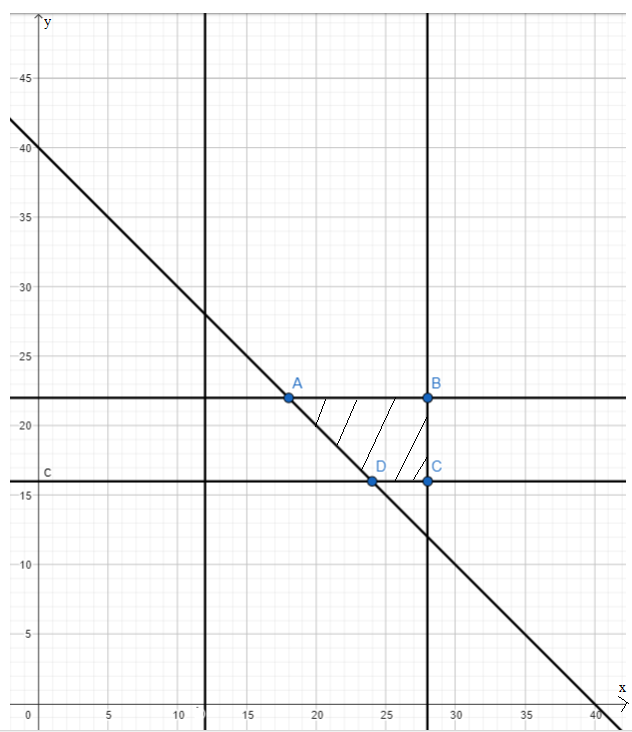
A(18; 22), B(28; 22), C(28; 16), D(24; 16)

Ta có: 

F(18; 22) = 88,8.

F(28; 22) = 108,8.

F(28; 16) = 94,4.

F(24; 16) = 86,4.

Vậy để vé máy bay là ít nhất cần 24 đại diện đến từ Hà Nội và 16 đại diện từ Thành phố Hồ Chí Minh.

Bài 2.14 trang 33 chuyên đề toán 12

Một vật nặng có khối lượng m được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc . Trong Vật lí, ta biết rằng lực kéo F cần thiết để di chuyển vật được cho bởi công thức

trong đó g là gia tốc trọng trường và c là hệ số ma sát của bề mặt (Theo Sullivan and Miranda, Calculus, W.H.Freeman and Company, 2014). Chứng tỏ rằng lực kéo F nhỏ nhất khi tan = c.

Giải nhanh:

=>  

Khi đó lực kéo F đạt giá trị nhỏ nhất.

Bài 2.15 trang 45 chuyên đề toán 12

Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn lớn nhất)?

Giải nhanh:

Gọi khoảng cách từ người đến bức tường là x

Khoảng cách tính đến mép dưới bức tranh là:

Khoảng cách tính đến mép trên bức tranh là:

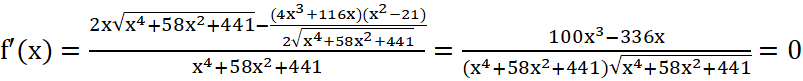
  x = 0 (loại) hoặc (thỏa mãn)

Vậy người quan sát phải đứng cách tường một khoảng tường là m thì tầm nhìn thuận lợi nhất.

Bài 2.16 trang 45 chuyên đề toán 12

Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở trung tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng cho bởi công thức , trong đó s là khoảng cách từ nguồn sáng và là góc mà ánh sáng chiếu vào bề mặt.

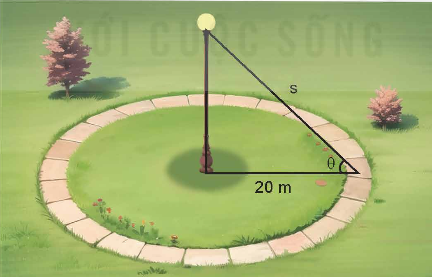
Giải nhanh:

Chiều cao của đèn là x (x > 0)

Cường độ chiếu sáng của đèn

(m)

=> ; l(0) = 0.

Vậy chiều cao cột là thì sẽ chiếu sáng mạnh nhất cho lối đi bộ.

Bài 2.17 trang 45 chuyên đề toán 12

Giả sử một loại hàng hóa có hàm cầu được mô hình hóa bởi p = 100 – 0,5x và hàm chi phí được mô hình hóa bởi C = 40x + 37,5, trong đó p (nghìn đồng) là giá của một đơn vị hàng hóa đó.

a) Mức giá nào sẽ mang lại lợi nhuận lớn nhất?

b) Khi lợi nhuận là lớn nhất, chi phí trung bình cho mỗi đơn vị là bao nhiêu?

Giải nhanh:

a) Hàm lợi nhuận là:

P(x) = x.p(x) – C(x) = x(100 – 0,5x) – 40x – 37,5 = -0,5x² + 60x – 37,5

P’(x) = -x + 60 = 0 => x = 60

=> P(x)_max tại x = 60 => P(60) = 1772,5 nghìn đồng

b) Chi phí trung bình cho mỗi đơn vị là:

C(x) = (nghìn đồng)