1. PHÉP THỬ LẶP VÀ CÔNG THỨC BERNOULLI

Hoạt động 1 trang 15 chuyên đề toán 12

Hình thành khái niệm phép thử lặp và công thức Bernoulli

Trong tình huống mở đầu. Xét phép thử T là gieo một xúc xắc cân đối, đồng chất. Gọi E là biến cố: “Xúc xắc xuất hiện mặt 6 chấm”.

a) Trong phương án 1, phép thử T được lặp lại bao nhiêu lần? Người chơi thắng khi biến cố E xuất hiện bao nhiêu lần?

b) Cũng hỏi như trên với phương án 2.

Giải nhanh:

a) Lặp lại 12 lần; Xuất hiện ít nhất 2 lần

b) Lặp lại 6 lần; Xuất hiện ít nhất 1 lần.

Luyện tập 1 trang 16 chuyên đề toán 12

Hai bạn An và Bình thi đấu bóng bàn. Xác suất thắng của An trong một ván là 0,4. Hai bạn thi đấu đủ 3 ván đấu. Người nào có số ván đấu thắng nhiều hơn là người thắng trận đấu đó. Giả sử các ván đấu là độc lập. Tính xác suất để An thắng trong trận đấu.

Giải nhanh:

Xác suất An thắng trận đấu = xác suất An thắng ít nhất hai ván đấu

Gọi biến cố A: “An thắng trận đấu đó”

Trường hợp 1: An thắng cả ba ván đấu => P₁ =

Trường hợp 2: An thắng 2 ván đấu => P₂ =

=>  P(A) = P₁ + P₂ = 0,064 + 0,288 = 0,352.

Luyện tập 2 trang 17 chuyên đề toán 12

Trở lại tình huống mở đầu.

a) Tính xác suất thắng của người chơi khi chơi theo phương án 2,

b) Qua các kết quả đã tính được, hãy cho biết người chơi nên chọn chơi theo phương án nào để xác suất thắng cao hơn.

Giải nhanh:

a) Xác suất nếu người chơi chọn phương án 1: P(B) 0,6187

Xác suất nếu người chơi chọn phương án 2:

Tương tự ví dụ 2, ta có: 

Xét phép thử lặp với n = 6 và P(E) =

=> P(

=> P(B) =

b) Phương án 2.

2. BIẾN NGẪU NHIÊN CÓ PHÂN BỐ NHỊ THỨC VÀ ÁP DỤNG

Hoạt động 2 trang 17 chuyên đề toán 12

Hình thành khái niệm biến ngẫu nhiên có phân bố nhị thức

Cho T là một phép thử và E là một biến cố liên quan tới phép thử T. Ta thực hiện phép thử T lặp lại n lần một cách độc lập. Ở mỗi lần thực hiện phép thử T, biến cố E có xác suất xuất hiện bằng p, tức là P(E) = p, 0 < p < 1. Gọi X là số lần xuất hiện biến cố E trog n lần thực hiện lặp lại phép thử T. Tính P(X = k) với mỗi k ; n}.

Giải nhanh:

Vận dụng công thức Bernoulli, ta có:

P(X = 0) =

P(X = 1) =

P(X = 2) =

=> P(X = k) =

=> P(X = n) =

Câu hỏi trang 17 chuyên đề toán 12

Viết bảng phân bố xác suất của biến ngẫu nhiên có phân bố Bernoulli

Giải nhanh:

Luyện tập 3 trang 18 chuyên đề toán 12

Khi tham gia một một trò chơi, người chơi gieo xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 5 lần. Mỗi lần gieo nếu số chấm xuất hiện lớn hơn 4 thì người chơi được 10 điểm. Tính xác suất để người chơi nhận được ít nhất 30 điểm.

Giải nhanh:

Phép thử T là: “Gieo một con xúc xắc cân đối, đồng chất”

Biến cố E: “Số chấm xuất hiện lớn hơn 4”

Ta có P(E) =

X là số lần xuất hiện biến cố E trong 5 lần thực hiện lặp lại phép thử T

=> Để được ít nhất 30 điểm thì X

Vận dụng trang 20 chuyên đề toán 12

Giải quyết bài toán ở tình huống mở đầu

Giải nhanh:

a) Gọi X là số câu trả lời đúng của An.

X là một biến ngẫu nhiên có phân bố nhị thức với tham số n = 10; p =

=> E(X) = np =

b) An vượt qua bài thi khi làm đúng ít nhất 5 câu =>

Theo chú ý về phân bố nhị thức ta có:

P(X

Xác suất vượt qua bài thi của An xấp xỉ là 7,81%.

3. BÀI TẬP CUỐI CHUYÊN ĐỀ

Bài 1.6 chuyên đề toán 12

Tại một nhà máy sản xuất linh kiện điện tử, các linh kiện được sắp xếp vào từng hộp một cách độc lập, mỗi hộp 10 linh kiện. Hộp được xếp loại I nếu hộp đó có nhiều nhất một linh kiện không đạt tiêu chuẩn. Biết rằng xác suất để nhà máy sản xuất ra một linh kiện điện tử không đạt tiêu chuẩn là 0,01. Hỏi tỉ lệ những hộp linh kiện điện tử loại I là bao nhiêu?

Giải nhanh:

X là số linh kiện không đạt tiêu chuẩn

X là một biến ngẫu nhiên có phân bố nhị thức với tham số n = 10, p = 0,01

Hộp được xếp loại I nếu hộp đó có nhiều nhất một linh kiện không đạt tiêu chuẩn =>

=> P(

Vậy tỉ lệ những hộp linh kiện điện tử loại I là 99,6%.

Bài 1.7 chuyên đề toán 12

Một bài thi trắc nghiệm gồm 10 câu hỏi, mỗi câu hỏi có 4 phương án trả lời, trong đó chỉ có một phương án đúng. Mỗi câu trả lời đúng được 4 điểm, mỗi câu trả lời sai trừ 1 điểm. Một thí sinh làm bài bằng cách ở mỗi câu hỏi chọn ngẫu nhiên một phương án trả lời. Tính xác suất để thí sinh đó sau khi hoàn thành hết 10 câu trong bài thi, có kết quả:

a) 15 điểm;

b) Bị âm điểm

Giải nhanh:

Gọi X là số câu trả lời đúng của thí sinh

X là một biến ngẫu nhiên có phân bố nhị thức với tham số n = 10; p =

a) 15 điểm => 5 câu đúng và 5 câu sai => X = 5

=> P = .

b) Bị âm điểm => trả lời đúng nhiều nhất 1 câu =>

=>

Bài 1.8 chuyên đề toán 12

Trong một trò chơi, mỗi ván người chơi gieo đồng thời 3 xúc xắc cân đối, đồng chất. Nếu có ít nhất 2 xúc xắc xuất hiện mặt 6 chấm thì người chơi giành chiến thắng ván chơi đó. Bác Hưng tham gia chơi 3 ván. Tính xác suất để bác Hưng thắng ít nhất 2 ván.

Giải nhanh:

Xác suất để một con xúc xắc xuất hiện mặt 6 chấm là

Gọi X là số con xúc xắc xuất hiện mặt 6 chấm.

Bác Hưng thắng cuộc 1 ván khi X ≥ 2.

=>

Gọi Y là số ván thắng của bác Hưng.

=>

Bài 1.9 chuyên đề toán 12

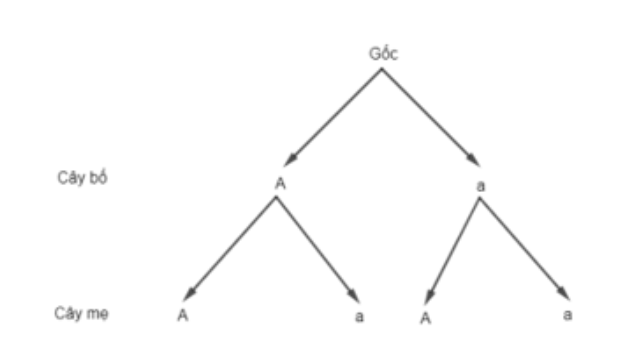
Màu hạt của đậu Hà Lan có hai kiểu hình: màu vàng và màu xanh. Có hai gene ứng với hai kiểu hình này là allele trội A và allele lặn a. Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. 

Bốn bạn An, Bình, Sơn và Dương, mỗi bạn độc lập với nhau, thực hiện phép thử là lai hai cây đậu Hà Lan, trong đó cây bố có kiểu gene là Aa, cây mẹ có kiểu gene là Aa.

Gọi X là số cây con có hạt màu vàng trong số 4 cây con.

a) Lập bảng phân bố xác suất của X.

b) Hỏi trung bình có bao nhiêu cây con có hạt màu xanh?

Giải nhanh:

a) Bảng phân bố xác suất của X

X	0	1	2	3	4
P

Giải thích:

X là một biến ngẫu nhiên có phân bố nhị thức n = 4; p =

Giá trị của X thuộc tập {0; 1; 2; 3; 4}

P(X = 0) =

P(X = 1) =

P(X = 2) =

P(X = 3) =

P(X = 4) =

b) Y là số cây con có hạt màu xanh

Y là biến ngẫu nhiên có phân bố nhị thức với tham số n = 4; P =

=> E(Y) = 4.

Bài 1.10 chuyên đề toán 12

Trong một lớp học có 6 bóng đèn hoạt động độc lập với nhau. Mỗi bóng có xác suất bị hỏng là 0,25. Gọi X là số bóng sáng.

a) Gọi tên phân bố xác suất biến ngẫu nhiên X.

b) Biết rằng lớp học có đủ ánh sáng nếu có ít nhất 4 bóng sáng. Tính xác suất để lớp học đủ ánh sáng.

c) Tính kì vọng, phương sai và độ lệch chuẩn của X.

Giải nhanh:

a) X là một biến ngẫu nhiên có phân bố nhị thức với tham số n = 6; p =

b) Ít nhất 4 bóng sáng => X ≥ 4

=>

c) E(X) = 6.

V(X) =

Bài 1.11 chuyên đề toán 12

Sơn và Tùng thi đấu bóng bàn với nhau. Trận đấu gồm 5 ván độc lập. Xác suất thắng của Sơn trong mỗi ván là . Biết rằng mỗi ván không có kết quả hòa. Người thắng trận đấu nếu thắng ít nhất 3 ván đấu.

a) Gọi X là số trận thắng của Sơn. Hỏi X là biến ngẫu nhiên có phân bố xác suất gì?

b) Tính xác suất để Sơn thắng Tùng trong trận đấu.

Giải nhanh:

a) X là biến ngẫu nhiên có phân bố xác suất nhị thức với tham số n = 5;

b) Sơn thắng Tùng trong trận đấu => X ≥ 3.

=> P( .

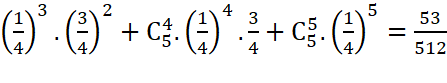Bài 1.12 chuyên đề toán 12

Cam xuất khẩu được đóng thành từng thùng. Xác suất để một quả cam không đạt chất lượng là 0,03. Vì số lượng cam trong mỗi thùng rất lớn nên không thể kiểm tra toàn bộ số cam trong thùng, người ta lấy ngẫu nhiên từ thùng cam 20 lần một cách độc lập, mỗi lần lấy 1 quả để kiểm tra rồi trả lại nó vào thùng. Gọi X là số quả cam không đạt chất lượng.

a) Gọi tên phân bố xác suất biến ngẫu nhiên X.

b) Các thùng cam được phân thành ba loại theo cách sau:

Trong 20 lần lấy đó:

- Nếu tất cả các quả cam lấy ra đều đạt chất lượng thì thùng được xếp loại I;

- Nếu có 1 hoặc 2 quả cam không đạt chất lượng thì thùng được xếp loại II;

- Nếu có ít nhất 3 quả cam không đạt chất lượng thì thùng được xếp loại III.

Tính tỉ lệ các thùng cam được xếp loại I, II, III.

Giải nhanh:

a) X là biến ngẫu nhiên có phân bố xác suất nhị thức với tham số n = 20; p = 0,03.

b) Thùng cam loại I nếu X = 0.

=> P₁ = P(X = 0) = ≈ 0,5438.

Thùng cam loại II nếu X = 1 hoặc X = 2: 

=> P₂ = P(X = 1) + P(X = 2) 

=

Thùng cam loại III nếu X ≥ 3.

=> P(X ≥ 3) = 1 – P₁ – P₂ = 1 – 0,5438 – 0,4352 = 0,021.