Giải bài: Ôn tập chương III - phương pháp tọa độ trong không gian
Đây là bài ôn tập chương 3, chương cuối cùng trong chương trình hình học 12 với nội dung: Phương pháp tọa độ trong không gian. Dựa vào cấu trúc SGK toán lớp 12, Tech12h sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn

A. Tổng hợp kiến thức
I. Biểu thức tọa độ của các phép toán vectơ
- Trong không gian Oxyz cho hai vectơ $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$. Ta có:
$\overrightarrow{a}+\overrightarrow{b}=(a_{1}+b_{1};a_{2}+b_{2};a_{3}+b_{3})$ $\overrightarrow{a}-\overrightarrow{b}=(a_{1}-b_{1};a_{2}-b_{2};a_{3}-b_{3})$ $k\overrightarrow{a}=k(a_{1};a_{2};a_{3})$ với k là số thực |
==> Hệ quả:
$\overrightarrow{a}=\overrightarrow{b}<=>a_{1}=b_{1};a_{2}=b_{2};a_{3}=b_{3}$ $\overrightarrow{0}=(0;0;0)$ $\overrightarrow{a},\overrightarrow{b}$ cùng phương <=> $a_{1}=kb_{1};a_{2}=kb_{2};a_{3}=kb_{3}$ $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(x_{B}-x_{A};y_{B}-y_{A};z_{B}-z_{A})$ |
II. Tích vô hướng
Định lí
- Trong không gian Oxyz, tích vô hướng của hai vectơ $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$ xác định bởi:
| $\overrightarrow{a}.\overrightarrow{b}=(a_{1}.b_{1}+a_{2}.b_{2}+a_{3}.b_{3})$ |
Ứng dụng
- Độ dài vectơ:
| $\overrightarrow{a}=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$ |
- Khoảng cách giữa hai điểm: Trong không gian Oxyz cho $A(x_{A},y_{A},z_{A})$ và $B(x_{B},y_{B},z_{B})$, ta có:
| $AB=\left | \overrightarrow{AB} \right |=\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ |
- Góc giữa hai vectơ: Góc giữa $\overrightarrow{a}(a_{1};a_{2};a_{3})$ và $\overrightarrow{b}(b_{1};b_{2};b_{3})$ là $\varphi $
| $\cos\varphi =\cos (\overrightarrow{a},\overrightarrow{b})=\frac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}$ |
- Đặc biệt:
| $\overrightarrow{a}\perp \overrightarrow{b}<=> a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=0$ |
III. Phương trình mặt cầu
Định lí
- Trong không gian Oxyz, mặt cầu S có tâm I( a; b; c ) bán kính r có phương trình là:
| $(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2}$ |
IV. Phương trình mặt phẳng
- Phương trình tổng quát của mặt phẳng:
| $Ax+By+Cz+D=0$ với $A,B,C\neq 0$. |
Điều kiện hai mặt phẳng song song, vuông góc
1. Điều kiện hai mặt phẳng song song
- $(\alpha _{1})//(\alpha _{2})<=>\left\{\begin{matrix}\overrightarrow{n_{1}}=k\overrightarrow{n_{2}} & \\ D_{1}\neq kD_{2} & \end{matrix}\right.<=> \left\{\begin{matrix}(A_{1};B_{1};C_{1})=k(A_{2};B_{2};C_{2}) & \\ D_{1}\neq kD_{2} & \end{matrix}\right.$
- $(\alpha _{1})\equiv (\alpha _{2})<=>\left\{\begin{matrix}\overrightarrow{n_{1}}=k\overrightarrow{n_{2}} & \\ D_{1}= kD_{2} & \end{matrix}\right.<=> \left\{\begin{matrix}(A_{1};B_{1};C_{1})=k(A_{2};B_{2};C_{2}) & \\ D_{1}= kD_{2} & \end{matrix}\right.$
- $(\alpha _{1})$ cắt $(\alpha _{2})$ <=> $\overrightarrow{n_{1}}\neq k\overrightarrow{n_{2}}<=>(A_{1};B_{1};C_{1})\neq k(A_{2};B_{2};C_{2}) $
2. Điều kiện hai mặt phẳng vuông góc
- $(\alpha _{1})\perp (\alpha _{2})<=>\overrightarrow{n_{1}}.\overrightarrow{n_{2}}=0<=>A_{1}.A_{2}+B_{1}.B_{2}+C_{1}.C_{2}=0$
Khoảng cách từ một điểm đến một mặt phẳng
Định lí
- Trong không gian Oxyz, cho mp($(\alpha )$ có phương trình $Ax+By+Cz+D=0$ và điểm $M_{0}(x_{0};y_{0};z_{0})$. Khoảng cách từ M đến mp($(\alpha )$ xác định bởi công thức:
| $d(M_{0},(\alpha ))=\frac{\left | Ax_{0}+By_{0}+Cz_{0}+D \right |}{\sqrt{A^{2}+B^{2}+C^{2}}}$ |
V. Phương trình tham số của đường thẳng
- Điều kiện cần và đủ để điểm $M(x;y;z)$ nằm trên $\Delta $ là có một số thực $t$ sao cho:
| $\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$ |
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau
1. Hai đường thẳng song song
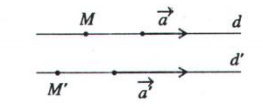
- d // d' <=> $d//d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \notin d' & & \end{matrix}\right.$
- $d \equiv d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \in d' & & \end{matrix}\right.$
2. Hai đường thẳng cắt nhau
Cho d: $\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$ và d': $\left\{\begin{matrix}x=x_{0}'+t'a_{1}' & & \\ y=y_{0}'+t'a_{2}' & & \\ z=z_{0}'+t'a_{3}' & & \end{matrix}\right.$
- $d$ và $d'$ cắt nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ có đúng một nghiệm.
3. Hai đường thẳng chéo nhau
- $d$ và $d'$ chéo nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ vô nghiệm.
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận