Chuyên đề bài toán thực tế (tiếp)
Câu 1: Cho biết sự tăng dân số được ước tính theo công thức $S=A.e^{Nr}$ (trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau N năm, r là tỉ lệ tăng dân số hàng năm). Đầu năm 2010, dân số tỉnh Bắc Ninh là 1.038.229 người, tính đến đầu năm 2015 dân số của tỉnh là 1.153.600 người. Hỏi nếu tỉ lệ tăng dân số hàng năm giữ nguyên thì đầu năm 2025 dân số của tỉnh nằm trong khoảng nào?
A. $(1.424.300; 1.424.400)$. | B. $(1.424.000; 1.424.100)$ |
| C. $(1.424.200; 1.424.300)$. | D. $(1.424.100; 1.424.200)$. |
Câu 2: Các loài cây xanh trong quang hợp sẽ nhận được một lượng nhỏ cacbon 14 (một đồng vị cacbon). Khi một bộ phận cây của cây đó bị chết thì hiện tượng quang hợp cũng sẽ ngưng và nó sẽ không nhận thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phân đó sẽ bị phân hủy một cách chậm chạp, chuyển hóa thành Nito 14. Gọi P(t) là số phần trăm cacbon 14 còn lại trong một bộ phận của cây sinh trưởng từ t năm trước đây thì p(t) được cho bởi công thưc $P(t)=100.0,5^{\frac{t}{5750}}(%)$. Phân tích một mẫu gỗ từ một công trình kiến trúc cổ người ta thấy được lượng cacbon 14 còn lại trong gỗ là 65,21%. Hãy xác định niên đại của công trình kiến trúc đó.
| A. 3574 năm. | B. 3754 năm. | C. 3475 năm. | D. 3547 năm. |
Câu 3: Huyện A có 100 000 người. Với mức tăng dân số bình quân là 1.5% năm thì sau n năm dân sô sẽ vượt lên 130 000 người. Hỏi n nhỏ nhất là bao nhiêu?
| A. 18 năm. | B. 17 năm. | C. 19 năm. | D. 16 năm. |
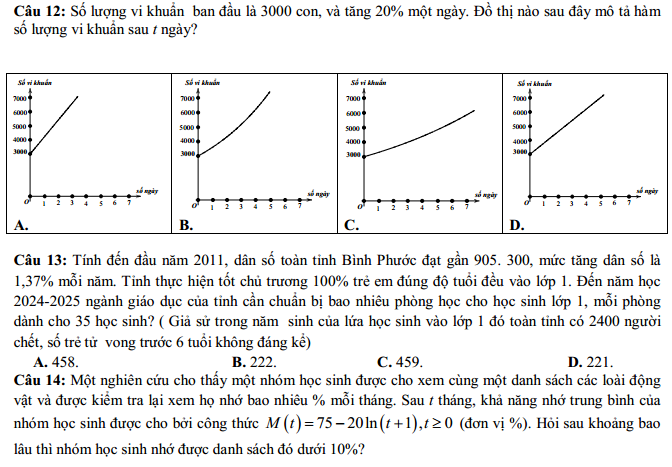
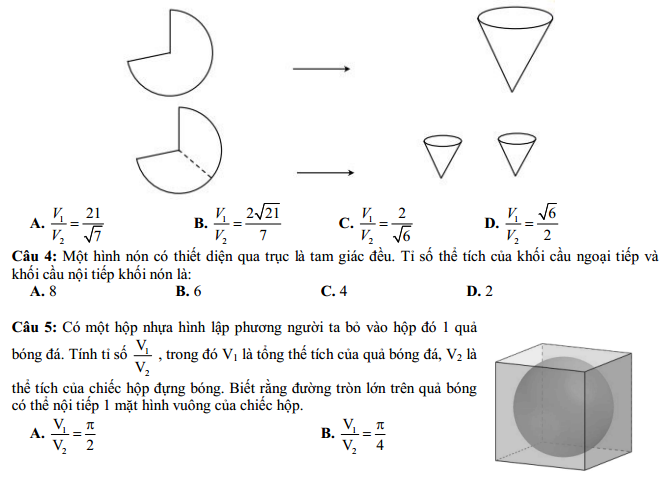
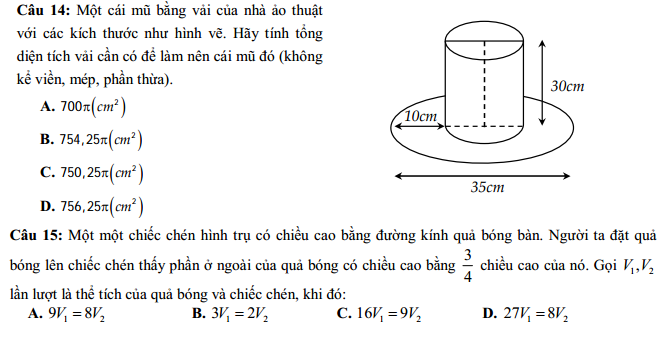
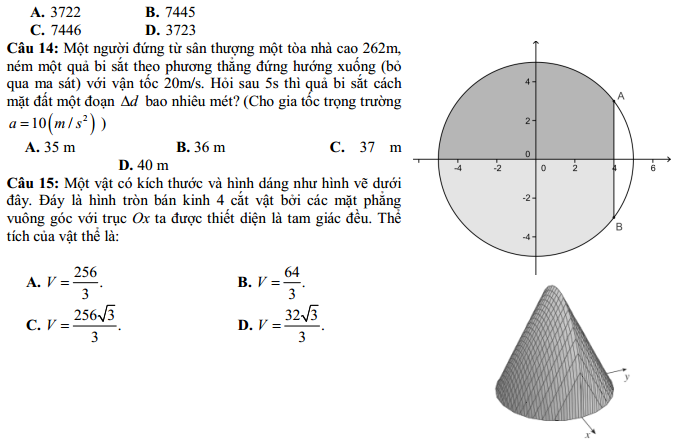
DẠNG 3: CÁC BÀI TOÁN ỨNG DỤNG HÀM SỐ MŨ- LÔGARIT












Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận