Nội dung bài viết gồm hai phần:

• Lý thuyết
• Hướng dẫn giải một số bài tập

A. Lý thuyết

1. Định nghĩa

Con lắc lò xo là hệ thống bao gồm 1 lò xo có độ cứng K, nó có khối lượng không đáng kể, có 1 đầu cố định và đầu còn lại gắn với 1 vật nặng có khối lượng m đặt theo phương ngang hoặc theo phương thẳng đứng.

2. Phương trình dao động

Con lắc lò xo có phương trình dao động: $x = A.\cos (\omega t + \varphi )$

Tần số góc: $\omega  = \sqrt{\frac{K}{m}}$

Chu kì dao động của con lắc lò xo: $T = 2\pi \sqrt{\frac{m}{K}} = 2\pi \sqrt{\frac{\Delta l}{g}} $

3. Lực hồi phục (Lực kéo về)

Lực gây ra trong dao động điều hòa của con lắc lò xo luôn luôn hướng về vị trí cân bằng được gọi là lực kéo về hay còn gọi là lực hồi phục. Lực kéo về này có độ lớn tỉ lệ với li độ dao động và chính là lực này gây ra gia tốc cho sự dao động điều hòa của con lắc lò xo.

Biểu thức: $F = - K.x = - m.\omega ^{2}.x$

Chú ý:

1. Lực hồi phục tỉ lệ thuận với độ cứng của lò xo, không phụ thuộc vào khối lượng vật.
2. Đối với con lắc lò xo nằm ngang, lực hồi phục chính là lực đàn hồi.
3. Đối với con lắc lò xo thẳng đứng hoặc nằm trên mặt phẳng nghiêng, lực hồi phục là lực tổng hợp tác dụng vào vật, luôn có xu hướng kéo vật về vị trí cân bằng.

3. Lực đàn hồi

Lực đàn hồi đối với con lắc lò xo nằm trên mặt phẳng nghiêng và con lắc lò xo thẳng đứng:

• Chiều dương hướng xuống: F_đh = k. $\left | \Delta l + x \right |$
• Chiều dương hướng lên: $\left | \Delta l - x \right |$

Các giá trị cực đại, cực tiểu của lực đàn hồi:

• Lực đàn hồi cực đại: F_{đh max}  = k. ($\Delta l + A$) (lực kéo): Lúc vật ở vị trí thấp nhất.
• Lực đàn hồi cực tiểu:
• A < $\Delta l$ F_đh ­­_min = k($\Delta l - A$)
• A $\geq $ $\Delta l$ F_{đh min}  = 0 (Lúc vật qua vị trí lò xo không biến dạng)

4. Các loại năng lượng của con lắc lò xo:

• Động năng của con lắc lò xo:

$W_{đ} = \frac{1}{2}.m.v^{2} = \frac{1}{2}.m.\omega ^{2}.A^{2}.\sin ^{2}(\omega t + \varphi ) = \frac{1}{2}.m.\omega ^{2}.A^{2}.\frac{1 - \cos (2\omega  + 2\varphi )}{2}$

• Thế năng của con lắc lò xo:

$W_{t} = \frac{1}{2}.k.x^{2} = \frac{1}{2}.m.\omega ^{2}.A^{2}.\cos ^{2}(\omega t + \varphi ) = \frac{1}{2}.m.\omega ^{2}.A^{2}.\frac{1 + \cos (2\omega  + 2\varphi )}{2}$

• Cơ năng của con lắc lò xo:

$W = W_{t} + W_{đ} = \frac{1}{2}.m.\omega ^{2}.A^{2} = \frac{1}{2}.k.A^{2} = const$

Chú ý:

1. Động năng, thế năng của con lắc lò xo hoặc dao động điều hòa biến thiên điều hòa cùng tần số góc: $\omega ' = 2\omega $, tần số f ' = 2f và  chu kì $T' = \frac{T}{2}$.
2. Cơ năng của con lắc lò xo luôn tỉ lệ thuận với bình phương biên độ của dao động.
3. Cơ năng của con lắc lò xo luôn được bảo toàn nếu ta bỏ qua mọi ma sát.
4. Cơ năng của con lắc không phụ thuộc vào khối lượng vật.

5. Độ biến dạng và chiều dài của lò xo khi ở VTCB

•   Độ biến dạng của lò xo khi vật tại vị trí cân bằng:
• Con lắc lò xo treo thẳng đứng: $\Delta l = \frac{m.g}{K}$
• Con lắc lò xo nằm trên mặt phẳng nghiêng góc $\alpha $ so với phương ngang: $\Delta l = \frac{m.g\sin \alpha }{K}$
• l_cb = l₀ + $\Delta l$  ( trong đó l₀ là chiều dài tự nhiên của lò xo) Chiều dài của lò xo tại vị trí cân bằng:
• Chiều dài lớn nhất của lò xo tương ứng với vật tại vị trí thấp nhất: l_max = l₀ + $\Delta l$  + A = l_cb­ + A
• Chiều dài nhỏ nhất của lò xo tương ứng với vật tại vị trí cao nhất): l_min = l₀ + $\Delta l$  - A = l_cb­ - A
• Chiều dài của lò xo khi vật ở vị trí cân bằng: $l_{cb} = \frac{l_{max} + l_{min}}{2}$
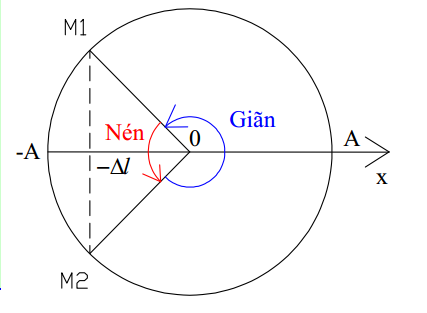
• Nếu A > $\Delta l$   (với Ox hướng xuống) ta xét trong một chu kì dao động thì:
• Thời gian lò xo nén sẽ tương ứng với vật đi từ điểm M₁ đến M₂.
• Thời gian lò xo dãn sẽ tương ứng với vật đi từ điểm M₂ đến M₁.

6. Cắt – ghép lò xo

a) Cắt lò xo

Một lò xo có độ cứng K, chiều dài l, được cắt thành các lò xo có độ cứng K₁, K₂, ... và chiều dài tương ứng l₁, l­₂, ...

Ta có: K.l = K₁.l₁ = K₂.l₂ = ...

b) Ghép lò xo

Giả sử cần ghép nối tiếp các lò xo có độ cứng K₁, K₂, .... Độ cứng của lò xo tương đương khi:

• Ghép nối tiếp: $\frac{1}{K} = \frac{1}{K_{1}} + \frac{1}{K_{2}} + ...$
• Ghép song song: K = K₁ + K₂ + ...

Chú ý: Khi treo vật có khối lượng m vào lò xo 1 thì vật dao động với chu kì T₁, treo vật vào lò xo 2 vật có chu kì dao động là T₂. Khi treo vật vào hệ lò xo thì chu kì dao động của vật là:

• Ghép nối tiếp: T²= T₁² + T₂²
• Ghép song song: $\frac{1}{T^{2}} = \frac{1}{T_{1}^{2}} + \frac{1}{T_{2}^{2}}$

7. Các dạng bài tập nâng cao về con lắc lò xo

a) Khi lò xo treo vật m₁ có chu kì T₁, vật m_2­ có chu kì T₂, vật có khối lượng (m­₁ + m­₂) có chu kì T₃, vật có khối lượng $\left | m_{1} - m_{2} \right |$ có chu kì T₄.

Mối liên hệ giữa T₁, T₂, T₃, T₄ là:

• T₃² = T₁²  + T­₂²
• T₄² = T₁² - T­₂²

b) Dạng bài tập về điều kiệ biên độ dao động

• Vật m₁ được đặt trên vật m­_{2 ­}dao động điều hòa theo phương thẳng đứng. Để m­­_1­ luôn nằm yên trên m­₂ trong quá trình dao động thì biên độ dao động của hệ thỏa mãn:

A $\leq  \frac{g}{\omega ^{2}} = \frac{(m_{1} + m_{2})g}{K}$

• Vật m₁ và m₂ được gắn vào hai đầu của lò xo đặt thẳng đứng, m₁ DĐĐH. Để m­₂ luôn nằm yên trên mặt sàn trong quá trình dao động thì biên độ dao động phải thỏa mãn:

A $\leq  \frac{g}{\omega ^{2}} = \frac{(m_{1} + m_{2})g}{K}$

• Vật m­₁ đặt trên m₂ DĐĐH theo phương ngang. Hệ số ma sát giữa hai vật là $\mu $, bỏ qua ma sát giữa vật với mặt sàn. Để m₁ không trượt trên m₂ trong quá trình dao động thì biên độ dao động thỏa mãn:

A $\leq  \mu \frac{g}{\omega ^{2}} = \mu \frac{(m_{1} + m_{2})g}{K}$