Nội dung bài viết gồm hai phần:

• Phương pháp giải bài tập
• Hướng dẫn giải một số bài tập mẫu

A. Lý thuyết

I. Phương pháp giải bài tập

Phương trình li độ, vận tốc trong dao động điều hòa:

• $x = A.\cos (\omega t + \varphi )$
• $v = -\omega A.\sin (\omega t + \varphi )$

1. Xác định quãng đường đi được từ t₁ đến t₂

Tính số chu kì dao động vật đi được từ thời điểm t₁ đến t­₂ là: $n = \frac{t_{2} - t_{1}}{T} = n,m$

• Nếu m = 0 thì:

Quãng đường vật đi được là: S₀ = 4.n.A

Số lần vật qua vị trí x₀ là: 2n

• Nếu m $\neq $ 0 thì:

Khi t = t₁, xác định trạng thái dao động của vật (li độ và chiều chuyển động)

Khi t = t₂, xác định trạng thái dao động của vật.

Dùng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều để xác định quãng đường S’ đi được và số lần z vật qua vị trí x₀ .

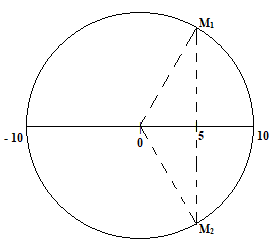
Khi đó, quãng đường vật đi được là: S = S₀ + S’

Số lần vật qua vị trí x₀ là: 2n + z (lần)

2. Xác định quãng đường lớn nhất mà vật đi được

Thực hiện các bước tương tự như trên với chú ý quãng đường lớn nhất vật đi được khi vật dao động quanh vị trí cân bằng

3. Xác định quãng đường nhỏ nhất vật đi được

Thực hiện các bước tương tự như trên với chú ý quãng đường nhỏ nhất vật đi được khi vật dao động quanh vị trí biên