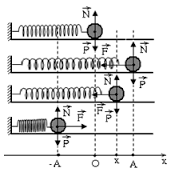
A. Lý thuyết

1, Bài toán liên quan đến tần số góc, chu kỳ, tần số

a)Tính chu kỳ, tần số, tần số góc khi cho m và k hoặc ngược lại

K là độ cứng của lò xo

$\omega =\sqrt{\frac{k}{m}}$       $T=2\pi \sqrt{\frac{m}{k}}$       $f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

Chu kỳ T tỉ lệ thuận với $\sqrt{m}$ và tỉ lệ nghịch với $\sqrt{k}$

b) Dạng thay đổi khối lượng vật nặng

• Trong cùng khoảng thời gian t, hai con lắc cùng thực hiện N₁ và N₂ dao động:

        $ f=\frac{N}{t}\Rightarrow \frac{k}{m}=\omega ^{2}=(2\pi f)^{2}=\left ( \frac{2\pi N}{t} \right )^{2}\Rightarrow \frac{m_{2}}{m_{1}}=\left ( \frac{N_{1}}{N_{2}}\right )^{2}$

• Thêm bớt khối lượng $\Delta m$:

       $\left ( \frac{\omega _{1}}{\omega _{2}} \right )^{2}=\left ( \frac{f_{1}}{f_{2}} \right )^{2}=\frac{m_{2}}{m_{1}}=\frac{m_{1}+\Delta m}{m_{1}}$

•  Ghép hai vật:

        $ m_{3}=m_{1}\pm m_{2}\rightarrow T_{3}^{2}=T_{1}^{2}\pm T_{2}^{2}$

c) Chu kỳ liên quan đến cắt ghe[s lò xo:

Sau khi ghép lò xo, chu kỳ của vật tính theo k_hệ qua biểu thức:

           $T=2\pi \sqrt{\frac{m}{k_{hệ}}}$

• Khi các lò xo mắc nối tiếp: $\frac{1}{k_{nt}}=\frac{}1{k_{1}}+\frac{1}{k_{2}}+\frac{1}{k_{3}}+...+\frac{1}{k_{n}}$

Suy ra: $T_{nt}^{2}=T_{1}^{2}+T_{2}^{2}+T_{3}^{2}+...+T_{n}^{2}$

• Khi các lò xo mắc song song:K_ss = k₁ + k₂ + k₃ + …+ k_n

Suy ra: $\frac{1}{T_{ss}^{2}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}+\frac{1}{T_{3}^{2}}+...+\frac{1}{T_{n}^{2}}$

•  Khi cắt lò xo ban đầu (l_o, k_o) thành hai lò xo (l₁, k₁ và l₂, k₂) thì l₁k₁ = l₂k₂ = l_ok_o

2, Viết phương trình dao động $x=A\cos (\omega t+\varphi )$

•  Tần số góc $\omega$: tùy vào từng dữ kiện bài toán mak tìm theo các cách khác nhau:

        $\omega =\frac{2\pi }{T}=2\pi f=\sqrt{\frac{k}{m}}=\sqrt{\frac{g}{\Delta l_{o}}}=\frac{v_{max}}{A}=\sqrt{\frac{a_{max}}{A}}=\left | \frac{a_{max}}{v_{max}} \right |$

•  Biên độ A:

        $A=\sqrt{\left ( \frac{v}{m} \right )^{2}+x^{2}}=\sqrt{\frac{2E}{k}}=\frac{\left [ v_{max} \right ]}{\omega }=\frac{\left [ a_{max} \right ]}{\omega ^{2}}=\frac{l_{max}-l_{min}}{2}$

• Pha ban đầu $\varphi$: dựa vào điều kiện ban đầu t=0:   $x_{o}=A\cos \varphi$

$y_{o}=-A\omega \sin \varphi$ $\Rightarrow \varphi $

Chú ý: nếu bài toán cho các giá trị x, v tại thời điểm t bất kì. Một trong những cách đơn giản là chỉ cần thay tất cả các giá trị t, x, v vào hệ pt của x và v rồi giả hệ

Trước khi tính $\varphi$ cần xác định rõ $\varphi$ thuộc góc phần tư thứ mấy trong vòng tròn lượng giác.

3, Dạng bài độ biến dạng và chiều dài của lò xo trong quá trình dao động

Chiều dài tự nhiên của là xo là l_o

•  Khi con lắc nằm ngang:
• Lúc ở VTCB, lò xo không bị biến dạng: $ \Delta l_{o}=0$
• Chiều dài cực đại của lò xo: l_max = l_o + A
• Chiều dài cực tiểu của lò xo: l_min = l_o – A
• Khi con lắc lò xo đươc bố trí nằm nghiêng một góc  $ \alpha$ vật treo ở dưới
•  Độ biến dạng  $ \Delta l_{o}$ của lò xo khi vật ở VTCB:  $\Delta l_{o}=\frac{mg\sin \alpha }{k}$

Nếu đặt thẳng đứng thì  $ \alpha=90^{o}$, $\sin \alpha=1$ nên:

    $\Delta l_{o}=\frac{mg }{k}=\frac{g}{\omega ^{2}}$

• Chiều dài lò xo khi ở VTCB : l_cb = l_o + $ \Delta l_{o}$
•  Chiều dài của li độ x:     l = l_o + $ \Delta l_{o}$ + x
• Chiều dài cực đại của lò xo : l_max = l_o + $ \Delta l_{o}$ + A
• Chiều dài cực tiểu của lò xo: l_min = l_o + $ \Delta l_{o}$ -A

4, Dạng bài tính lực đàn hồi

• Đặc điểm: luôn hướng về vị trí cân bằng.
• Biểu thức tính: F = -kx, trong đó x là li độ.

5, Dạng bài liên quan đến lực đàn hồi. Lực đàn hồi kéo – đẩy cực đại, cực tiểu

Lực đàn hồi là lực đưa vật về vị trí cần bằng sao cho lò xo có chiều dài tự nhiên l_o.

• Nếu con lắc lò xo bố trí nằm ngang, $ \Delta l_{o}=0$:
• Tại VTCB: x = 0, F_đhmin = 0
•  Tại vị trí biên: x_max = A, F_đhmax = kA
•  Nếu con lắc bố trí thẳng đứng:

    $\Delta l_{o}=\frac{mg }{k}=\frac{g}{\omega ^{2}}$

• Độ lớn lực đàn hồi cực đại (khi vật xuống thấp nhất): F_{kéo max} = $k\left |  \Delta l_{o}+A\right |$
• Độ lớn lực đàn hồi cực tiểu còn phụ thuộc vào độ lớn của A so với     $\Delta l_{o}$

Nếu A < $\Delta l_{o}$: Trong quá trình vật dao động, lò xo luôn dãn.   F_kéomin = $k\left | \Delta l_{o}-A \right |$

Nếu A  > $\Delta l_{o}$: Trong quá trình dao động, lò xo ngoài dãn còn nén

Lúc vật đi qua vị trí lò xo có chiều dài tự nhiên: F_đhmin = 0.

Lúc vật lên cao nhất, lò xo nén cực đại: F_đẩymax = $k\left | A-\Delta l_{o}\right |$

Lúc vật xuống thấp nhất, lò xo nén cực đại: F_kéomax = $k\left | \Delta l_{o}+A \right |$

6. Dạng bài liên quan đến tính khoảng thời gian lò xo nén hay giãn trong một chu kỳ khi vật treo ở dưới và  A  > $\Delta l_{o}$

Phương pháp: chuyển về bài toán quen thuộc là tìm thời thời gian vật đi từ li độ x₁ đến x₂. Tuy nhiên có thể tính nhanh như sau:

•  Khoảng thời gian nén: $ \Delta t=2\frac{\alpha }{\omega }$, với $\cos \alpha =\frac{\Delta l_{o}}{A}$
•  Khoảng thời gian lò xo dãn là: T - $\Delta T$

7. Dạng bài liên quan đến năng lượng dao động. Tính động năng, thế năng

•  Động năng vật nặng: W_đ = $\frac{1}{2}mv^{2}$

$=\frac{1}{2}mv^{2}=\frac{1}{2}mA^{2}\omega ^{2}\sin ^{2}(\omega t+\varphi )=\frac{1}{2}kA^{2}\frac{1-\cos 2(\omega t+\varphi )}{2}$

•  Thế năng lò xo: $W_{t}=\frac{1}{2}kx^{2}$, với   $k=m\omega ^{2}$

$W_{t}=\frac{1}{2}kx^{2}=\frac{1}{2}kA^{2}\cos ^{2}(\omega t+\varphi )=\frac{1}{2}kA^{2}\frac{1+\cos 2(\omega t+\varphi )}{2}$

•  Năng lượng: W = W_đ + W_t = W_đmax = $\frac{1}{2}mA^{2}\omega ^{2}$ = W_tmax = $\frac{1}{2}kA^{2}$

Tuy cơ năng không thay đổi nhưng động năng và thế năng biến thiên với $ {\omega }'=2\omega , {f}'=2f, {T}'=\frac{T}{2}$

Động năng và thế năng biến đổi qua lại với nhau, khi động năng của con lắc có giá trị gấp n lần thế năng ta được:

$(n+1)W_{t}=\frac{1}{2}kA^{2}\Rightarrow (n+1)\frac{1}{2}kx^{2}=\frac{1}{2}kA^{2}$

\Rightarrow$ x=\pm \frac{A}{\sqrt{n+1}}$

                    $v=\pm \sqrt{\frac{n}{n+1}}.v_{max}$

Đặc biệt, trong một chu kì có 4 lần W_đ = W_t, khoảng thời gian giữa hai lần liên tiếp để W_đ = W_t là $\Delta t=\frac{T}{4}$ . Khi W_đ = W_t thì $x=\pm \frac{A}{\sqrt{2}}$

8. Điều kiện của biên độ dao động

•  Vật m₁ được đặt trên vật m₂ dao động điều hòa theo phương thẳng đứng. Để m₁ luôn nằm yên trên m₂ trong quá trình dao động thì: $A\leq \frac{g}{\omega ^{2}}=\frac{(m_{1}+m_{2})g}{k}$
•  Vật m₁ và m₂ được gắn vào hai đầu của lò xo thẳng đứng, m₁ dao động điều hòa. Để m₂ luôn nằm yên trên mặt sàn trong quá trình dao động thì: $A\leq \frac{(m_{1}+m_{2})g}{k}$
• Vật m₁ được đặt trên m₂ dao động điều hòa theo phương ngang. Hệ số ma sát giữa m₁ và m2  là $\mu $ bỏ qua ma sát giữa m2 và mặt sàn. Để m1 không trượt trên m2 trong quá trình dao động thì:

$A\leq \mu \frac{g}{\omega ^{2}}=\mu \frac{(m_{1}+m_{2})g}{k}$

9. Dạng bài toán liên quan đến sư thay đổi của biên độ

$A_{2}=\sqrt{x_{2}^{2}+\frac{v_{2}^{2}}{\omega _{2}^{2}}}$

Nếu $x_{2}=0$ thì $v_{2max}=\omega _{2}A_{2}$

• Ngay trước thời điểm thay đổi thì vật có đại lượng là : $A_{1}, \omega_{1}, v_{1}, x_{1}$

Ngay sau thời điểm thay đổi thì các đại lượng của vật là: $A_{2}, \omega_{2}, v_{2}, x_{2}$

• Va chạm mềm: $m_{1}.v_{1}+m_{2}.v_{2}=(m_{1}+m_{2}).v$

Nếu m₂ đứng yên thì: $m_{1}.v_{1}=(m_{1}+m_{2}).v$

•  Va chạm đàn hồi: ${v_{1}}'=\frac{(m_{1}-m_{2})v_{1}+2m_{2}v_{2}}{m_{1}+m_{2}}$

                                 ${v_{2}}'=\frac{(m_{2}-m_{1})v_{2}+2m_{1}v_{1}}{m_{1}+m_{2}}$

•  Vật đang chuyển động mà nhấc vật ra theo phương vuông góc với phương chuyển động thì coi như ngược lại với va chạm mềm
•  Nếu vật đang chuyển động mà đặt thêm vật khác theo phương vuuong góc với vật thì coi đó là va chạm mềm
•  Vị trí cân bằng của con lắc lò xo nằm ngang là vị trí phần lò xo còn lại không biến dạng

 Vị trí cân bằng của con lắc lò xo thẳng đứng là $\overrightarrow{F_{hl}}=\overrightarrow{0}$