Bài 1: Toàn bộ lý thuyết về dao động cơ học
Trong bài học này, tech12h đã tổng kết lại toàn bộ kiến thức trọng tâm của dao động cơ học. Hi vọng với những nội dung kiến thức dưới đây các e có thể ôn tập lại một cách dễ dàng

A. Kiến thức trọng tâm
I. Khái niệm chung
Dao động cơ là chuyển động qua lại của vật quanh 1 vị trí cân bằng.
Dao động tuần hoàn là dao động mà sau những khoảng thời gian bằng nhau vật trở lại vị trí và chiều chuyển động như cũ (trở lại trạng thái ban đầu).
Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hoặc sin) của thời gian.
Dao động tự do (dao động riêng): Là dao động của hệ xảy ra dưới tác dụng chỉ của nội lực. Dao động riêng là dao động có tần số (tần số góc, chu kỳ) chỉ phụ thuộc các đặc tính của hệ không phụ thuộc các yếu tố bên ngoài. Khi đó: $\omega $ gọi là tần số góc riêng; f gọi là tần số riêng; T gọi là chu kỳ riêng
II. Các đại lượng của dao động điều hòa
1. Phương trình dao động điều hòa
Phương trình dao động: x = A.cos($\omega $t + $\varphi $)
Trong đó:
- x: là li độ (toạ độ) của vật; cho biết độ lệch và chiều lệch của vật so với VTCB. Đơn vị: m, cm
- A: Là biên độ của vật cho biết độ lệch cực đại của vật so với VTCB. Hay, A chính là độ lệch cực đại của vật. Đơn vị: m, cm
- ($\omega $t + $\varphi $) (rad): Là pha của dao động của vật tại thời điểm t; cho biết trạng thái dao động của vật ở thời điểm t.
- $\varphi $ (rad): Là pha ban đầu của dao động cho biết trạng thái ban đầu của vật.
- $\omega $ (rad/s): Là tần số góc của dao động điều hoà; cho biết tốc độ biến thiên góc pha
Chú ý: Trong dao động điều hòa:
- Biên độ luôn luôn dương: A > 0.
- Tần số góc luôn dương: $\omega $ > 0
- Trạng thái dao động của vật cho biết vị trí và chiều chuyển động.
2. Chu kì, tần số trong dao động điều hòa
Chu kì T (s): Là khoảng thời gian để thực hiện một dao động toàn phần. Chu kì chính là khoảng thời gian ngắn nhất để vật trở lại vị trí và chiều chuyển động như cũ (trở lại trạng thái ban đầu).
Tần số f (Hz): Là số dao động toàn phần thực hiện được trong một giây.
$f = \frac{1}{T}$
Mối liên hệ giữa tần số góc, chu kì và tần số trong dao động điều hòa:
$\omega = \frac{2\pi }{T} = 2\pi .f$
3. Vận tốc trong dao động điều hòa
Vận tốc là đạo hàm bậc nhất của li độ theo thời gian:
v = x' = - $\omega $Asin($\omega $t + $\varphi $) = $\omega $ A.cos($\omega $t + $\varphi $ + $\frac{\pi }{2}$)
Vận tốc của vật dao động điều hòa biến thiên điều hòa cùng tần số nhưng sớm pha hơn $\frac{\pi }{2}$so với với li độ.
Các vị trí đặc biệt của vận tốc:
- Ở vị trí biên (x = ± A): Độ lớn vận tốc của vật là: |v|= 0
- Ở vị trí cân bằng (x = 0): Độ lớn vận tốc của vật là: |v| = $\omega $A.
Giá trị đại số:
- vmax = $\omega $A khi v > 0 (vật qua VTCB theo chiều dương)
- vmin = - $\omega $A khi v < 0 (vật qua vị trí cân bằng theo chiều âm)
4. Gia tốc trong dao động điều hòa
Gia tốc là đạo hàm bậc nhất của vận tốc (đạo hàm bậc 2 của li độ) theo thời gian:
a = v' = x’’ = - $\omega $2A.cos($\omega $t + $\varphi $) = - $\omega $2x
Gia tốc của vật dao động điều hòa biến thiên điều hòa cùng tần số nhưng ngược pha với li độ (sớm pha $\frac{\pi }{2}$ so với vận tốc)
Véc tơ gia tốc của vật dao động điều hòa luôn hướng về vị trí cân bằng và tỉ lệ với độ lớn của li độ.
Các vị trí đặc biệt của gia tốc
- Ở vị trí biên (x = ± A): gia tốc có độ lớn cực đại : |a|max = $\omega $2A.
- Giá trị đại số: amax= $\omega $2A khi x = - A; amin= - $\omega $2A khi x = A;.
- Ở vị trí cân bằng (x = 0): gia tốc bằng 0.
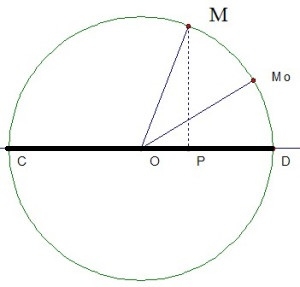
5. Mối liên hệ giữa dao động điều hòa và chuyển động tròn đều
Điểm P dao động điều hòa trên một đoạn thẳng luôn luôn có thể dược coi là hình chiếu của một điểm M chuyển động tròn đều trên đường kính là đoạn thẳng đó.
Đồ thị của dao động điều hòa là một đường hình sin.
Quỹ đạo dao động điều hoà là một đoạn thẳng.
6. Lực trong dao động điều hòa
Trong dao động điều hòa, lực hồi phục luôn hướng về vị trí cân bằng và là lực gây ra dao động cho vật.
Fhp = - k.x
Đặc điểm: Luôn luôn ngược với chiều chuyển động.
7. Năng lượng trong dao động điều hòa (Cơ năng)
Thế năng trong dao động điều hòa: Wt = $\frac{1}{2}.m.\omega ^{2}.x^{2}$
Động năng trong dao động điều hòa: Wđ = $\frac{1}{2}.m.v^{2}$
Cơ năng của dao động điều hòa: W = Wđ + Wt = const
8. Chú ý:
- Vận tốc luôn cùng chiều với chiều chuyển động.
- Gia tốc luôn hướng về VTCB.
- Hệ thức độc lập với thời gian: A2 = x2 + $(\frac{v}{\omega })^{2}$
- Dao động điều hòa có tần số góc $\omega $, tần số f, chu kì T thì động năng và thế năng biến thiên với tần số góc 2 $\omega $, tần số 2f, chu kì T/2.
- Quãng đường vật đi được trong 1 chu kì là 4A, trong 1/2 chu kì luôn là 2A.

Bình luận