Soạn giáo án điện tử Toán 12 KNTT Bài 6: Vectơ trong không gian

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC 

MÔN TOÁN!

KHỞI ĐỘNG

Ở lớp 10, ta đã biết về vectơ trong mặt phẳng và biết sử dụng vectơ để biểu thị đại lượng có hướng và độ lớn trong mặt phẳng, ví dụ như vận tốc hay lực. Đối với các đại lượng có hướng trong không gian, ta có thể sử dụng vectơ để biểu diễn chúng hay không? Các phép toán vectơ trong trường hợp này giống và khác như thế nào với các phép toán vectơ trong   mặt phẳng?

CHƯƠNG II. VECTƠ VÀ HỆ TRỤC TỌA ĐỘ TRONG KHÔNG GIAN 

BÀI 6. VECTƠ TRONG 

KHÔNG GIAN 

NỘI DUNG BÀI HỌC

1. VECTƠ TRONG KHÔNG GIAN

• HĐ1: Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ. 

a) Các đoạn thẳng này cho biết gì về hướng và độ lớn của các lực căng dây?

b) Các đoạn thẳng này có cùng nằm trên một mặt phẳng không?

Giải:

a) Các đoạn thẳng có mũi tên màu đỏ thể hiện rằng lực căng dây nằm dọc theo dây treo và hướng về phía móc treo của cần cẩu. Độ lớn của các lực căng dây là xấp xỉ bằng nhau.

b) Các đoạn thẳng không cùng nằm trong một mặt phẳng.

Định nghĩa 

• Vectơ trong không gian là một đoạn thẳng có hướng.
• Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

Hình 2.3 cho ta ví dụ về một số đại lượng có thể được biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự.

Trả lời:

Lực kéo của sợi dây tác động lên thùng hàng.

Chú ý: Tương tự như vectơ trong mặt phẳng, đối với vectơ trong không gian ta cũng có các kí hiệu và khái niệm sau:

• Vectơ có điểm đầu là và điểm cuối là được kí hiệu là .
• Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ thì vectơ còn được kí hiệu là
• Độ dài của vectơ được kí hiệu là ,          độ dài của vectơ được kí hiệu là .
• Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

     Ví dụ 1.

Cho tứ diện có độ dài mỗi cạnh bằng .

a) Có bao nhiêu vectơ có điểm đầu là và điểm cuối là một trong các đỉnh còn lại của tứ diện?

b) Trong các vectơ tìm được ở câu a, những vectơ nào có giá nằm trong mặt phẳng ?

c) Tính độ dàu của các vectơ tìm được ở câu a.

Giải:

a) Có ba vectơ là và .

b) Trong ba vectơ và chỉ có hai vectơ và có giá nằm trong       mặt phẳng

c) Vì tứ diện có độ dài mỗi cạnh bằng nên

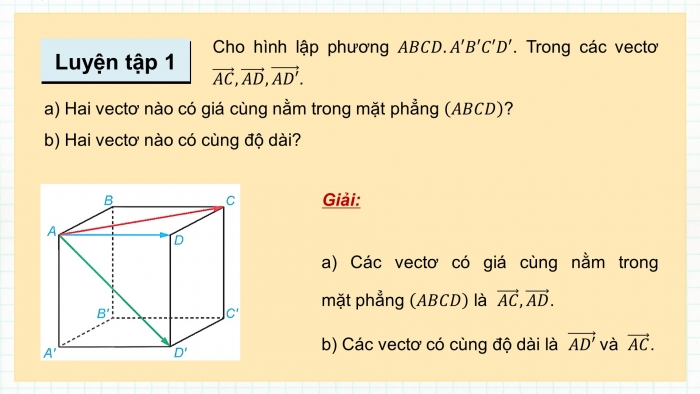
Luyện tập 1

Cho hình lập phương . Trong các vectơ .

a) Hai vectơ nào có giá cùng nằm trong mặt phẳng ?

b) Hai vectơ nào có cùng độ dài?

Giải:

a) Các vectơ có giá cùng nằm trong          mặt phẳng là  .

b) Các vectơ có cùng độ dài là  và  .

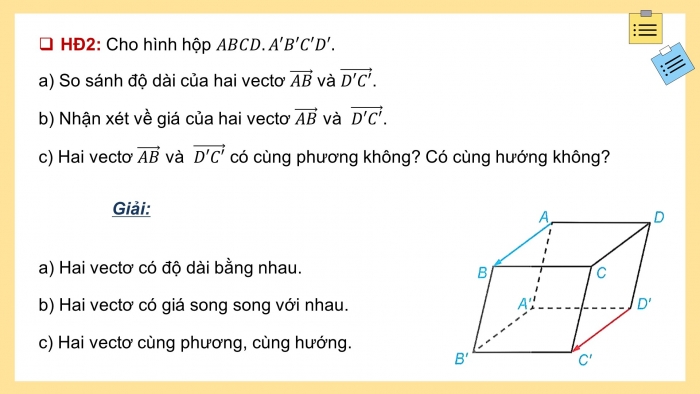
• HĐ2: Cho hình hộp

a) So sánh độ dài của hai vectơ và .

b) Nhận xét về giá của hai vectơ và  .

c) Hai vectơ và   có cùng phương không? Có cùng hướng không?

Giải:

a) Hai vectơ có độ dài bằng nhau.

b) Hai vectơ có giá song song với nhau.

c) Hai vectơ cùng phương, cùng hướng.

Ghi nhớ

• Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
• Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
• Hai vectơ và được gọi là bằng nhau, kí hiệu , nếu chúng có cùng độ dài và cùng hướng.

Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?

Trả lời:

Hai vectơ cùng bằng một vectơ thứ ba thì chúng bằng nhau vì chúng có cùng hướng và cùng độ dài.

Chú ý: Tương tự như vectơ trong mặt phẳng, ta có tính chất và các quy ước sau đối với vectơ trong không gian.

• Trong không gian, với mỗi điểm và vectơ cho trước, có duy nhất một điểm sao cho  .
• Các vectơ có điểm đầu và điểm cuối trùng nhau, ví dụ như   gọi là các vectơ-không.
• Ta quy ước vectơ-không có độ dài là 0, cùng hướng (và vì vậy cùng phương) với mọi vectơ. Do đó, các vectơ-không đều bằng nhau và được kí hiệu chung là .

     Ví dụ 2.

Cho hình lăng trụ

a) Trong ba vectơ , vectơ nào bằng vectơ ? Giải thích tại sao.

Giải:

Hai đường thẳng và chéo nhau nên hai vecto và không cùng phương. 

Do đó, hai vectơ và không bằng nhau.

Tứ giác là hình bình hành nên và Hai vecto và có cùng độ dài và cùng hướng nên hai vectơ đó bằng nhau.

Tương tự, hai vectơ và có cùng độ dài và ngược hướng nên hai vectơ và không bằng nhau.

b) Gọi là trung điểm của cạnh . Xác định điểm sao cho .

Gọi là trung điểm của cạnh . 

Vì tứ giác là hình bình hành nên và

Hình lăng trụ có và suy ra và .

Hai vecto và có cùng độ dài và cùng hướng nên .

Vậy trung điểm của cạnh là điểm cần tìm.

Luyện tập 2

Cho hình chóp có đáy là là hình bình hành.

a) Trong ba vectơ vectơ nào bằng vectơ ?

b) Gọi là một điểm thuộc cạnh . Xác định điểm sao cho .

Giải:

a) Vì là hình bình hành nên // và . Khi đó: .

b) Để   thì // và . 

Suy ra, là hình bình hành. 

Khi đó, điểm thuộc cạnh sao cho .

Vận dụng 1

Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao?

Giải:

Nếu biểu thị vị trí của thang máy ở các tầng 15, 22, 29 lần lượt bởi các điểm thì vectơ biểu thị độ dịch chuyển của thang máy trong hai lần di chuyển là và . 

Vì thẳng hàng theo thứ tự nên và cùng hướng. 

Hơn nữa và đều có độ dài bằng tổng chiều cao của 7 tầng nên . 

Vậy .

2. TỔNG VÀ HIỆU CỦA HAI VECTƠ TRONG KHÔNG GIAN

--------------- Còn tiếp ---------------