Soạn giáo án điện tử Toán 12 KNTT Bài 1: Tính đơn điệu và cực trị của hàm số

Nội dung giáo án

CHÀO MỪNG CÁC EM 
ĐẾN VỚI TIẾT HỌC 
MÔN TOÁN!

KHỞI ĐỘNG

Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí (mét) của chất điểm trên trục số đã chọn tại thời điểm (giây) được cho bởi công thức: 

Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

(H.1.1)

CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ 

HÀM SỐ

BÀI 1. TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ

NỘI DUNG BÀI HỌC

01

TÍNH ĐƠN ĐIỆU 
CỦA HÀM SỐ

a) Khái niệm tính đơn điệu của hàm số

• HĐ1: Nhận biết tính đồng biến, nghịch biến của hàm số

Quan sát đồ thị của hàm số (H.1.2).

a) Hàm số đồng biến trên khoảng nào? 

b) Hàm số nghịch biến trên khoảng nào?

Trả lời:

a) Hàm số đồng biến trên khoảng .

b) Hàm số nghịch biến trên khoảng .

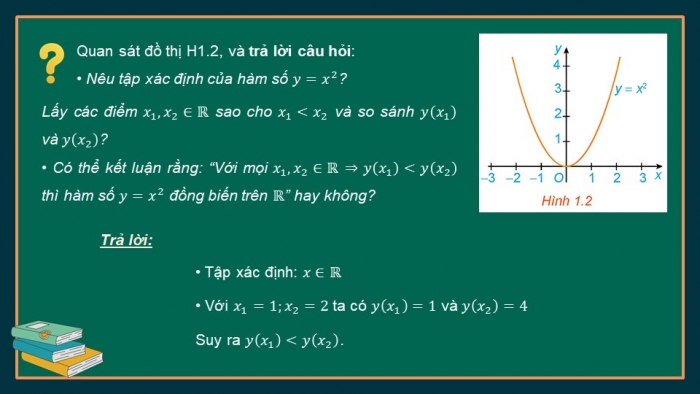
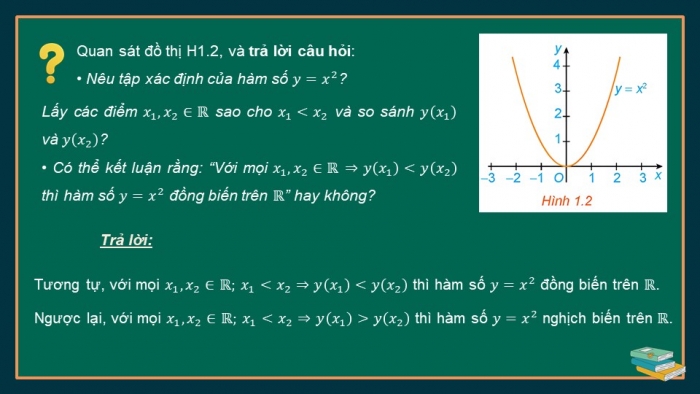
Quan sát đồ thị H1.2, và trả lời câu hỏi:

• Nêu tập xác định của hàm số ?

Lấy các điểm sao cho và so sánh và ? 

• Có thể kết luận rằng: “Với mọi thì hàm số đồng biến trên ” hay không?

Trả lời:

• Tập xác định:

• Với ta có và  

Suy ra .

Tương tự, với mọi thì hàm số đồng biến trên .

Ngược lại, với mọi thì hàm số nghịch biến trên .

Ghi nhớ

Giả sử là một khoảng, một đoạn hoặc một nửa khoảng và là hàm số xác định trên .

• Hàm số được gọi là đồng biến trên nếu ,
• Hàm số được gọi là nghịch biến trên nếu , .

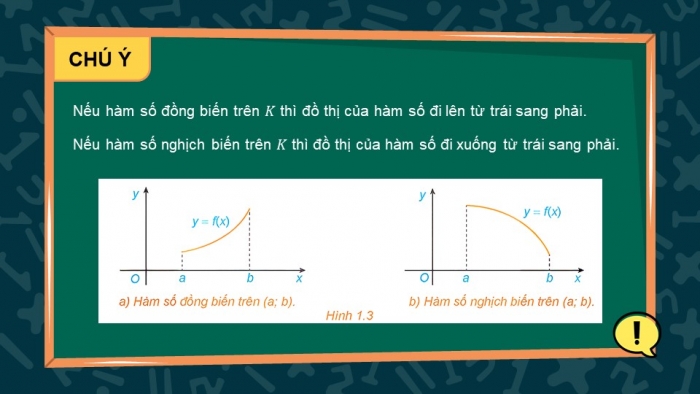
CHÚ Ý

Nếu hàm số đồng biến trên thì đồ thị của hàm số đi lên từ trái sang phải.

Nếu hàm số nghịch biến trên thì đồ thị của hàm số đi xuống từ trái sang phải.

• Hàm số đồng biến hay nghịch biến trên còn được gọi chung là đơn điệu trên . Việc tìm khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.
• Xét tính đơn điệu của hàm số mà không chỉ rõ tập thì ta hiểu là xét trên tập xác định của hàm số.

Ví dụ 1. Hình 1.4 là đồ thị của hàm số Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.

Giải:

Tập xác định của hàm số là .

Từ đồ thị suy ra: Hàm số đồng biến trên khoảng nghịch biến trên khoảng

Luyện tập 1

Hình 1.5 là đồ thị của hàm số . Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.

Giải:

• Hàm số đồng biến trên và
• Hàm số nghịch biến trên .

• HĐ2: Nhận biết mối quan hệ giữa tính đơn điệu và dấu của đạo hàm

Xét hàm số  có đồ thị như Hình 1.6. 

a) Xét dấu đạo hàm của hàm số trên các khoảng Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.

b) Có nhận xét gì về đạo hàm và hàm số trên khoảng ?

Trả lời:

a) Trên khoảng , đạo hàm mang dấu âm Hàm số nghịch biến.

     Trên khoảng , đạo hàm mang      dấu dương Hàm số đồng biến.

b) Trên khoảng , đạo hàm bằng 0 

Hàm số không đổi.

ĐỊNH LÍ

Cho hàm số có đạo hàm trên khoảng .

a) Nếu với mọi thì hàm số đồng biến trên khoảng .

b) Nếu với mọi thì hàm số nghịch biến trên khoảng .

• Định lí trên vẫn đúng trong trường hợp bằng tại một số hữu hạn điểm trong khoảng .
• Người ta chứng minh được rằng, nếu với mọi thì hàm số không đổi trên khoảng .

Ví dụ 2. Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số

Giải:

Tập xác định của hàm số là . 

Ta có: với

                       với

Do đó, hàm số đồng biến trên khoảng

                        nghịch biến trên khoảng

Luyện tập 2

Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số

Giải:

• Tập xác định:
• Ta có:

với ; với .

Vậy, hàm số đồng biến trên khoảng và hàm số nghịch biến trên khoảng .

b) Sử dụng bảng biến thiên xét tính đơn điệu của hàm số

• HĐ3: Xét tính đơn điệu của hàm số bằng bảng biến thiên

Cho hàm số

a) Tính đạo hàm và tìm các điểm mà

b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.

c) Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Trả lời:

Tập xác định:

a)

b) Bảng biến thiên:

Các bước để xét tính đơn điệu của hàm số :

--------------- Còn tiếp ---------------