Vẽ hai đường thẳng xy và mn cắt nhau tại điểm O sao cho $\widehat{xOm}=120^{\circ}$.

- Ta có $\widehat{yOm}+\widehat{mOx}=180^{\circ}$ (hai góc kề bù) hay $\widehat{yOm}+120^{\circ}=180^{\circ}$ do đó $\widehat{yOm}=180^{\circ}-120^{\circ}=60^{\circ}$.

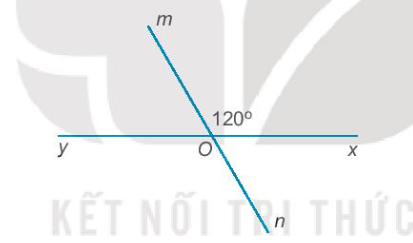
- Ta có $\widehat{yOn}=\widehat{mOx}=120^{\circ}$ (hai góc đối đỉnh).

- Ta có $\widehat{xOn}=\widehat{mOy}=60^{\circ}$ (hai góc đối đỉnh).