Giải câu 48 bài: Luyện tập sgk Toán đại 9 tập 2 Trang 59
Câu 48: trang 59 sgk toán lớp 9 tập 2
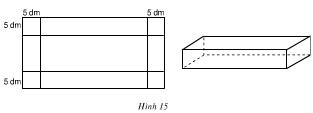
Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông có cạnh bằng \(5\) dm để làm thành một cái thùng hình hộp chữ nhật không nắp có dung tích \(1500\) dm3 (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp đôi chiều rộng.
Gọi chiều rộng của miếng tôn là \(x\) (dm), \(x > 0\).
Chiều dài của nó là \(2x\) (dm)
Khi làm thành một cái thùng không đáy thì chiều dài của thùng là \(2x - 10\) (dm), chiều rộng là \(x - 10\) (dm), chiều cao là \(5\) (dm).
(Vì khi người ta cắt ở bốn góc bốn hình vuông cạnh 5dm thì chiều dài và chiều rộng đều giảm đi 10dm)
Dung tích của thùng là$1500 dm^{3}$
Ta có phương trình: \(5(2x - 10)(x - 10)=1500\) (dm3)
$\Leftrightarrow (10x-50)(x-10)=1500$
$\Leftrightarrow 10x^{2}-100x-50x+500-1500=0$
$\Leftrightarrow 10x^{2}-150x-1000=0$
$\Leftrightarrow x^{2}-15x-100=0$
Giải phương trình
\(\Delta = (-15)^{2}-4.1.(-100)=225 + 400 = 625\)
\(\Rightarrow \sqrt{\Delta} = \sqrt{625}=25\)
\(\Rightarrow \left[ \matrix{x_{1}=\frac{-(-15)+25}{2} \hfill \cr x_{2}=\frac{-(-15)-25}{2} \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{x_{1}=20 \hfill \cr x_{2}=-10 \hfill \cr} \right.\)
Kết hợp với điều kiện ban đầu ta thấy $x_{2}=-10$không thỏa mãn.
Chiều dài miếng tôn là $20.2=40(dm)$
Vậy miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40 (dm).
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận