Giải bài 7.25 bài ba đường conic
Bài tập 7.25. Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B.
a. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế.
b. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế.
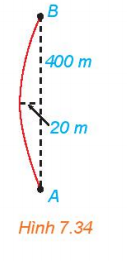

Chọn hệ trục tọa độ sao cho đỉnh của parabol trùng với gốc tọa độ O(0; 0) (như hình vẽ).
a. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế thì tọa độ các điềm là: A(20; -200) và B(20; 200) thuộc vào parabol có dạng y2 = 2px
Thay tọa độ điểm A và ta có: 2002 = 2p.20 $\Rightarrow$ 2p = 2000
Vậy parabol có dạng: y2 = 2000.x
b. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế thì tọa độ các điềm là: A(0,02; -0,2) và B(0,02; 0,2) thuộc vào parabol có dạng y2 = 2px
Thay tọa độ điểm A và ta có: 0,22 = 2p.0,02 $\Rightarrow$ 2p = 2
Vậy parabol có dạng: y2 = 2.x
Xem toàn bộ: Giải bài 22 Ba đường conic

Bình luận