Giải bài 4 trang 33 SBT toán 10 tập 1 chân trời

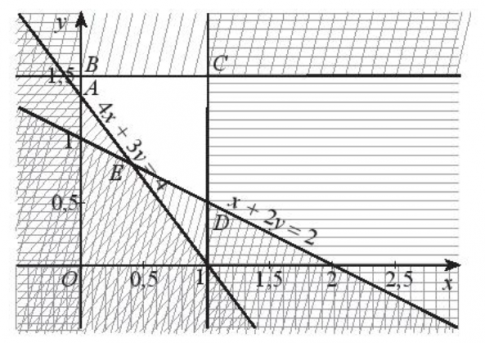
Gọi x và y lần lượt là số ki-lô-gam thịt bò và thịt heo có thể mua. Ta có hệ bất phương trình sau:

$\left\{\begin{matrix}4x+3y ≥ 4 &  & \\ x + 2y ≥ 2 &  & \\ x ≥ 0 &  & \\ x ≤ 1 &  & \\ y ≥ 0 &  & \\ y ≤ 1,5 &  & \end{matrix}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình ta được miền đa giác ABCDE có toạ độ các đỉnh là: A(0; $\frac{4}{3}$) ; B(0; $\frac{3}{2}$) ; C(1; $\frac{3}{2}$) ; D(A; $\frac{1}{2}$ ; E($\frac{2}{5}$; $\frac{4}{5}$)

Số tiền người đó thu được F = 250x + 200y đạt GTNN là 260 nghìn đồng tại đỉnh E ($\frac{2}{5}$ ; $\frac{4}{5}$).

Vậy gia đình này chỉ cần mua $\frac{2}{5}$ kg thịt bò và $\frac{4}{5}$ kg thịt heo để đủ đáp ứng yêu cầu về dinh dưỡng mà lại tốn chi phí ít nhất.