Giải bài 3 trang 27 SBT toán 10 tập 1 chân trời

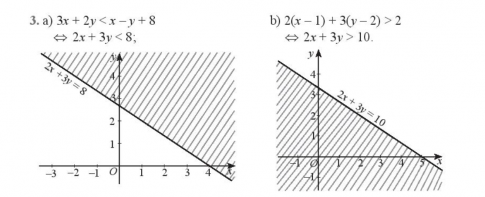
a) Ta có : 3x + 2y < x – y + 8

⇔ 3x – x + 2y + y < 8

⇔ 2x + 3y < 8.

Vẽ đường thẳng 2x + 3y = 8.

Cho x = 0, khi đó 2 . 0 + 3y = 8, suy ra y = 8383.

Cho y = 0, khi đó 2x + 3 . 0 = 8, suy ra x = 4.

Vì vậy, đường thẳng 2x + 3y = 8 đi qua hai điểm (0; 83) và (4; 0).

Lấy điểm O(0; 0) không thuộc đường thẳng 2x + 3y = 8.

Ta có: 2 . 0 + 3 . 0 = 0 < 8, do đó tọa độ điểm O thỏa mãn bất phương trình 2x + 3y < 8.

Vậy miền nghiệm của bất phương trình 2x + 3y < 8 là nửa mặt phẳng có bờ là đường thẳng 2x + 3y = 8, chứa gốc O và không kể đường thẳng 2x + 3y = 8.

b) 2(x – 1) + 3(y – 2) > 2

⇔ 2x – 2 + 3y – 6 > 2

⇔ 2x + 3y > 10.

Vẽ đường thẳng 2x + 3y = 10.

Cho x = 0, khi đó 2 . 0 + 3y = 10, suy ra y = 103103.

Cho y = 0, khi đó 2x + 3 . 0 = 10, suy ra x = 5.

Vì vậy, đường thẳng 2x + 3y = 10 đi qua hai điểm (0; 103) và (5; 0).

Lấy điểm O(0; 0) không thuộc đường thẳng 2x + 3y = 10.

Ta có: 2 . 0 + 3 . 0 = 0 < 10, do đó tọa độ điểm O không thỏa mãn bất phương trình 2x + 3y > 10.

Vậy miền nghiệm của bất phương trình 2x + 3y > 10 là nửa mặt phẳng có bờ là đường thẳng 2x + 3y = 10, không chứa gốc O và không kể đường thẳng 2x + 3y = 10.