Đáp án câu 4 đề 1 kiểm tra học kì 2 Toán 9

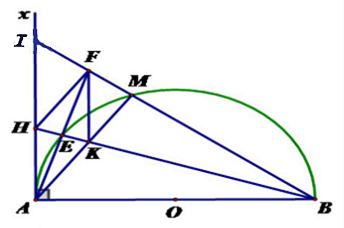
a, Có AB là đường kính của nửa đường tròn (O), M, E là 2 điểm trên nửa đường tròn

$\Rightarrow \widehat{AEB} = \widehat{AMB} = 90^{\circ}$

Do đó tứ giác AEMB nội tiếp.

Ax là tiếp tuyến tại A của đường tròn (O) $\Rightarrow Ax \perp AB$ hay $\Rightarrow AI \perp AB$ ($I\in Ax$) $\Rightarrow \Delta AIB$ vuông tại A

$\widehat{AMB} = 90^{\circ}$ nên $AM \perp MB$ hay $AM \perp IB$ ( do I, M, B thẳng hàng)

Xét tam giác AIB vuông tại A có $AM \perp IB \Rightarrow AI^{2} = IM.IB$ (đpcm)

b, Ta có: $\widehat{EAM}$ và $\widehat{EBM}$ là hai góc nội tiếp chắn cung EM.

$\Rightarrow \widehat{EAM} = \widehat{EBM}$ (1)

AF là phân giác của góc $\widehat{IAM} \Rightarrow \widehat{IAF} = \widehat{FAM}$ (2)

$\widehat{IAF}$ là góc tạo bởi tia tiếp tuyến Ax và dây cung AE, $\widehat{ABE}$ là góc nội tiếp chắn cung AE $\Rightarrow \widehat{IAF} = \widehat{ABE}$ (3)

Từ (1), (2) và (3) $\Rightarrow \widehat{ABE} = \widehat{EBF}$. Mà tia BE nằm trong $\widehat{BFA}$

$\Rightarrow$ BE là tia phân giác của $\widehat{ABF}$

Vậy BE là đường phân giác của $\Delta BAF$

Mà $AE\perp EB$ nên $\Delta BAF$ là tam giác cân tại B (vì BE vừa là đường cao vừa là đường phân giác của $\Delta BAF$).

c, $\Delta BAF$ là tam giác cân tại B có BE là đường cao nên BE là đường trung trực của AF. Hay HK là đường trung trực của AF.

$\Rightarrow$ FK = AK và HA = HF (*)

Xét $\Delta HKA$ có AE là phân giác của $\widehat{HAK}$ và $AE \perp HK$ nên AE là đường trung trực của HK hay AF là đường trung trực của HK

$\Rightarrow $ HA = AK và HF = FK (**)

Từ (*) và (**) ta được HA = AK = KF = FH

Do đó tứ giác AKHF là hình thoi (đpcm).