Đáp án câu 2 đề 1 kiểm tra học kì 2 Toán 9

a, Xét hàm số: y = $x^{2}$ (P)

Tập xác định: R

Bảng giá trị

Đồ thị hàm số y = $x^{2}$ là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và điểm O(0;0) là đỉnh và là điểm thấp nhất.

Xét hàm số: y = - x + 2 (d)

Tập xác định R

Bảng giá trị

Đồ thị hàm số y = - x + 2 là đường thẳng đi qua 2 điểm (0; 2) và (2; 0).

Ta có đồ thị 2 hàm số trên trục tọa độ

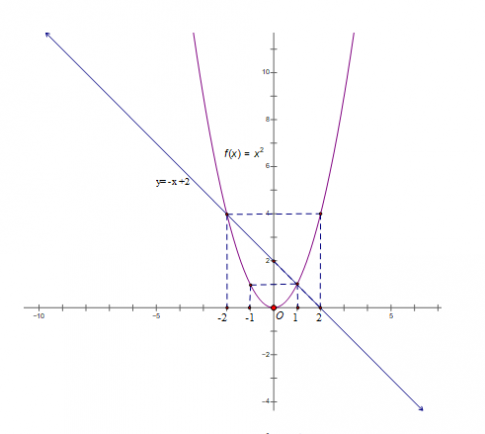
b, Phương trình hoành độ giao điểm của (P) và (d) là:

$x^{2} = -x + 2 \Leftrightarrow  x^{2} + x - 2 = 0 \Leftrightarrow (x - 1)(x + 2) = 0 \Leftrightarrow$ x = 1 hoặc x = -2

+, x = 1 ⇒ y = 1

+, x = -2 ⇒ y = 4

Vậy tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)

c, Do d' // d nên phương trình của d' có dạng: y = -x + b (b ≠ 2)

Gọi A là giao điểm của d' và (P) và A có hoành độ -1 

Có A(-1; $y_{A}$) thuộc (P): y = $x^{2} \Rightarrow y_{A} = 1$

Do A (-1; 1) \in d $ \Rightarrow$  1 = -(-1) + b $\Rightarrow$  b = 0

⇒ Phương trình đường thẳng d' là y = -x.