Cho Hình 4.16, biết rằng $\widehat{DAC}=40^{\circ},\widehat{DCA}=50^{\circ}$, hãy tính số đo các góc của tam giác ABC.

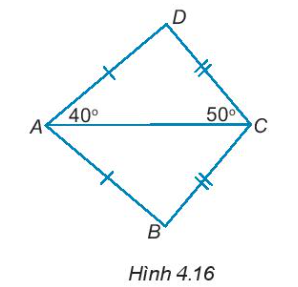
Xét tam giác ADC có:

$\widehat{DAC}+\widehat{DCA}+\widehat{D}=180^{\circ}$ (định lí tổng ba góc trong tam giác)

$40^{\circ}+50^{\circ}+\widehat{D}=180^{\circ}$

$\widehat{D}=180^{\circ}-40^{\circ}-50^{\circ}=90^{\circ}$

Xét $\Delta ADC$ và $\Delta ABC $có:

AD = AB (giả thiết)

DC = BC (giả thiết)

AC chung

Do đó, $\Delta ADC = \Delta ABC$ (c . c . c)

Suy ra, $\widehat{DAC}=\widehat{BAC};\widehat{DCA}=\widehat{BCA};\widehat{D}=\widehat{B} $(các góc tương ứng).

Do đó, $\widehat{BAC}=\widehat{DAC}=40^{\circ};\widehat{DCA}=\widehat{BCA}=50^{\circ};\widehat{B}=\widehat{D}=90^{\circ}$.

Vậy tam giác ABC có $\widehat{BAC}=40^{\circ};\widehat{BCA}=50^{\circ};\widehat{B}=90^{\circ}$.