CHƯƠNG VI: HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG

BÀI 15. HÀM SỐ

1. KHÁI NIỆM HÀM SỐ

HĐ1: 

a)

• Thời điểm 8 giờ: 57,9.

• Thời điểm 12 giờ: 69,07.

• Thời điểm 16 giờ: 81,78.

b) Mỗi thời điểm tương ứng với một giá trị của nồng độ bụi PM 2.5.

HĐ2: 

a) Từ năm 2013 đến năm 2019.

b) Năm mực nước cao nhất: 2013 và 2018 (242mm).

Năm mực nước thấp nhất: 2015 (237mm).

Kết luận:

Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D gọi là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá tri của hàm số.

Ví dụ 1 (SGK -tr6)

Ví dụ 2 (SGK -tr6)

Ví dụ 3 (SGK -tr6)

Luyện tập 1:

a) 

Bảng 6.4 có cho ta một hàm số vì mỗi giá trị của x cho ta tương ứng một và chỉ một giá trị của y.

Tập xác định: D = {2013;2014;2015;2016;2017;2018}

Tập giá trị: {73,1; 73,2; 73,3; 73,4; 73,5}

b) Giá trị hàm số tại x = 2018 là y = 242.

c) f(1) = -2.1$^{2}$=-1

f(2) = -2.2$^{2}$=-8

Tập xác định: D=R

Do x$^{2}$≥0,∀x∈R nên -2.x$^{2}$≤0,∀x∈R.

Tập giá trị: (-∞;0].

Nhận xét:

Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc mô tả bằng lời.

2. ĐỒ THỊ CỦA HÀM SỐ

HĐ4:

Những điểm nằm trên đồ thị của hàm số  y=$\frac{1}{2}$x$^{2}$ là:  (0; 0), (2; 2), (-2; 2).

Nhận xét: tung độ bằng bình phương hoành độ nhân với $\frac{1}{2}$.

Kết luận:

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x: f(x)) trên mặt phẳng tọa độ với mọi x thuộc D.

Ví dụ 4 (SGK -tr7)

Luyện tập 2:

a) y=8⇔$\frac{1}{2}$x$^{2}$=8⇔x$^{2}$=16⇔x=±4.

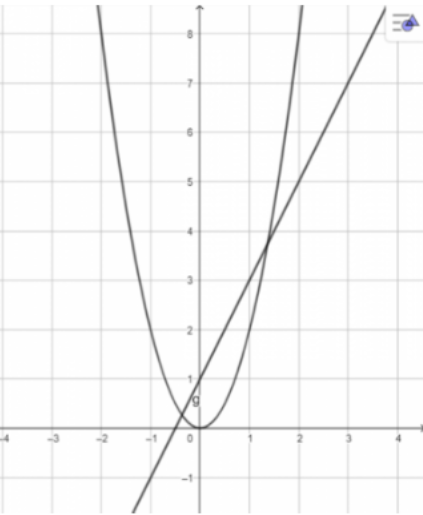
b) 

+ Đồ thị hàm số y = 2x + 1

x = 0 ⇒ y = 1;

x = 1 ⇒ y = 3

+ Đồ thị hàm số  y = 2x$^{2}$ 

x = 0 ⇒ y = 0 

x=1⇒y=2; x=-1⇒y=2

x=2 ⇒y=8; x=-2⇒y=8.

Vận dụng 1:

Đường màu đen là đồ thị ở Hình 6.3, đường màu đỏ là đồ thị hàm số y = 1,734x - 2,8 trên tập D=(50; 100].

3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

HĐ5: (Bảng phía dưới)

Khi x tăng, y tương ứng của hàm y = -x+1 giảm.

Khi x tăng, y tương ứng của hàm y = x tăng.

HĐ6: 

a) f(x) tăng

b) f(x) giảm.

Định nghĩa:

Hàm số y=f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu:

$\forall x_{1}$,x$_{2}$ $\in $(a;b), x$_{1}$< x$_{2}$=> f(x$_{1}$)<f(x$_{2}$)

Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu:

$\forall x_{1}$,x$_{2}$ $\in $(a;b), x$_{1}$< x$_{2}$=> f(x$_{1}$)> f(x$_{2}$)

Ví dụ 5 (SGK -tr8)

Chú ý:

+ Đồ thị của một hàm số đồng biến trên khoảng (a; b) là đường "đi lên" từ trái sang phải.

+ Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường "đi xuống" từ trái sang phải.

Luyện tập 3:

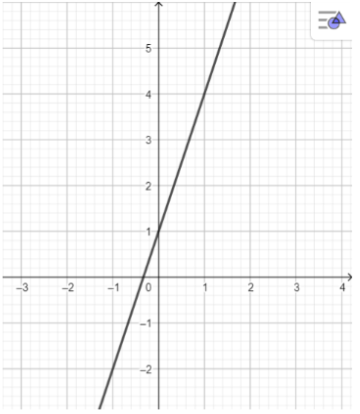
Đồ thị hàm số y=3x+1

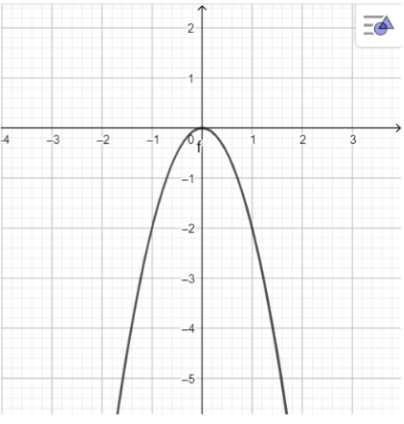
Đồ thị hàm số y = -2x$^{2}$

a) Hàm số đồng biến trên  R, vì đồ thị đi lên từ trái sang phải.

b) Hàm số đồng biến trên khoảng (-∞;0) vì đồ thị đi lên từ trái sang phải. 

Hàm số nghịch biến trên khoảng (0;+∞) vì đồ thị đi xuống từ trái sang phải.

Vận dụng 2: 

a) Số tiền phải trả khi di chuyển 25 km là: 10 000+13 000(25-0,6)=327 200 đồng.

b) 

Gọi x là số kilomet mà xe taxi di chuyển. (đơn vị: km), (x > 0).

Gọi y là số tiền cước taxi phải trả theo x kilomet di chuyển. (đơn vị: nghìn đồng), (x≥10)

y=$\left\{\begin{matrix}10,x\leq 0,6 & \\ 10+13(x-0,6); 0,6<x\leq 25 & \\ 10+13.24,4+11(x-25); x>25 & \end{matrix}\right.$

Hay 

y=$\left\{\begin{matrix}10,x\leq 0,6 & \\ 13x+2,2;  0,6<x\leq 25 & \\ 11x+52,2; x>25 & \end{matrix}\right.$

c)

Hàm số đồng biến trên khoảng (0,6;+∞)